travel time dilation formula

Time Dilation

Samuel J. Ling; Jeff Sanny; and William Moebs

Learning Objectives

By the end of this section, you will be able to:

• Explain how time intervals can be measured differently in different reference frames.
• Describe how to distinguish a proper time interval from a dilated time interval.
• Describe the significance of the muon experiment.
• Explain why the twin paradox is not a contradiction.
• Calculate time dilation given the speed of an object in a given frame.

The analysis of simultaneity shows that Einstein’s postulates imply an important effect: Time intervals have different values when measured in different inertial frames. Suppose, for example, an astronaut measures the time it takes for a pulse of light to travel a distance perpendicular to the direction of his ship’s motion (relative to an earthbound observer), bounce off a mirror, and return ( (Figure) ). How does the elapsed time that the astronaut measures in the spacecraft compare with the elapsed time that an earthbound observer measures by observing what is happening in the spacecraft?

Examining this question leads to a profound result. The elapsed time for a process depends on which observer is measuring it. In this case, the time measured by the astronaut (within the spaceship where the astronaut is at rest) is smaller than the time measured by the earthbound observer (to whom the astronaut is moving). The time elapsed for the same process is different for the observers, because the distance the light pulse travels in the astronaut’s frame is smaller than in the earthbound frame, as seen in (Figure) . Light travels at the same speed in each frame, so it takes more time to travel the greater distance in the earthbound frame.

Time dilation is the lengthening of the time interval between two events for an observer in an inertial frame that is moving with respect to the rest frame of the events (in which the events occur at the same location).

The lengths D and L in (Figure) are the sides of a right triangle with hypotenuse s . From the Pythagorean theorem,

Note that we used Einstein’s second postulate by taking the speed of light to be c in both inertial frames. We substitute these results into the previous expression from the Pythagorean theorem:

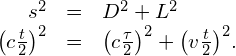
Then we rearrange to obtain

This is equivalent to

and v and c are the speeds of the moving observer and light, respectively.

This time effect is real and is not caused by inaccurate clocks or improper measurements. Time-interval measurements of the same event differ for observers in relative motion. The dilation of time is an intrinsic property of time itself. All clocks moving relative to an observer, including biological clocks, such as a person’s heartbeat, or aging, are observed to run more slowly compared with a clock that is stationary relative to the observer.

Half-Life of a Muon

Before we present the first example of solving a problem in relativity, we state a strategy you can use as a guideline for these calculations.

• Make a list of what is given or can be inferred from the problem as stated (identify the knowns). Look in particular for information on relative velocity v .
• Identify exactly what needs to be determined in the problem (identify the unknowns).
• Make certain you understand the conceptual aspects of the problem before making any calculations (express the answer as an equation). Decide, for example, which observer sees time dilated or length contracted before working with the equations or using them to carry out the calculation. If you have thought about who sees what, who is moving with the event being observed, who sees proper time, and so on, you will find it much easier to determine if your calculation is reasonable.
• Determine the primary type of calculation to be done to find the unknowns identified above (do the calculation). You will find the section summary helpful in determining whether a length contraction, relativistic kinetic energy, or some other concept is involved.

Note that you should not round off during the calculation . As noted in the text, you must often perform your calculations to many digits to see the desired effect. You may round off at the very end of the problem solution, but do not use a rounded number in a subsequent calculation. Also, check the answer to see if it is reasonable: Does it make sense? This may be more difficult for relativity, which has few everyday examples to provide experience with what is reasonable. But you can look for velocities greater than c or relativistic effects that are in the wrong direction (such as a time contraction where a dilation was expected).

Time Dilation in a High-Speed Vehicle The Hypersonic Technology Vehicle 2 (HTV-2) is an experimental rocket vehicle capable of traveling at 21,000 km/h (5830 m/s). If an electronic clock in the HTV-2 measures a time interval of exactly 1-s duration, what would observers on Earth measure the time interval to be?

Strategy Apply the time dilation formula to relate the proper time interval of the signal in HTV-2 to the time interval measured on the ground.

Significance The very high speed of the HTV-2 is still only 10 -5 times the speed of light. Relativistic effects for the HTV-2 are negligible for almost all purposes, but are not zero.

What Speeds are Relativistic? How fast must a vehicle travel for 1 second of time measured on a passenger’s watch in the vehicle to differ by 1% for an observer measuring it from the ground outside?

Strategy Use the time dilation formula to find v/c for the given ratio of times.

• Identify the unknown: v/c .

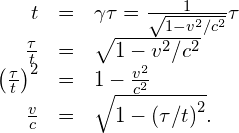
Significance The result shows that an object must travel at very roughly 10% of the speed of light for its motion to produce significant relativistic time dilation effects.

As we will discuss later, in the muon’s reference frame, it travels a shorter distance than measured in Earth’s reference frame.

Significance The time of travel is extremely short, as expected. Because the calculation is entirely within a single frame of reference, relativity is not involved, even though the electron speed is close to c .

Strategy for (b) (b) In the frame of reference of the electron, the vacuum tube is moving and the electron is stationary. The electron-emitting cathode leaves the electron and the front of the vacuum tube strikes the electron with the electron at the same location. Therefore we use the time dilation formula to relate the proper time in the electron rest frame to the time in the television frame.

Significance The time of travel is shorter in the electron frame of reference. Because the problem requires finding the time interval measured in different reference frames for the same process, relativity is involved. If we had tried to calculate the time in the electron rest frame by simply dividing the 0.200 m by the speed, the result would be slightly incorrect because of the relativistic speed of the electron.

Check Your Understanding

The Twin Paradox

The paradox here is that the two twins cannot both be correct. As with all paradoxes, conflicting conclusions come from a false premise. In fact, the astronaut’s motion is significantly different from that of the earthbound twin. The astronaut accelerates to a high velocity and then decelerates to view the star system. To return to Earth, she again accelerates and decelerates. The spacecraft is not in a single inertial frame to which the time dilation formula can be directly applied. That is, the astronaut twin changes inertial references. The earthbound twin does not experience these accelerations and remains in the same inertial frame. Thus, the situation is not symmetric, and it is incorrect to claim that the astronaut observes the same effects as her twin. The lack of symmetry between the twins will be still more evident when we analyze the journey later in this chapter in terms of the path the astronaut follows through four-dimensional space-time.

In 1971, American physicists Joseph Hafele and Richard Keating verified time dilation at low relative velocities by flying extremely accurate atomic clocks around the world on commercial aircraft. They measured elapsed time to an accuracy of a few nanoseconds and compared it with the time measured by clocks left behind. Hafele and Keating’s results were within experimental uncertainties of the predictions of relativity. Both special and general relativity had to be taken into account, because gravity and accelerations were involved as well as relative motion.

• Two events are defined to be simultaneous if an observer measures them as occurring at the same time. They are not necessarily simultaneous to all observers—simultaneity is not absolute.
• Time dilation is the lengthening of the time interval between two events when seen in a moving inertial frame rather than the rest frame of the events (in which the events occur at the same location).

• The premise of the twin paradox is faulty because the traveling twin is accelerating. The journey is not symmetrical for the two twins.
• Time dilation is usually negligible at low relative velocities, but it does occur, and it has been verified by experiment.
• The proper time is the shortest measure of any time interval. Any observer who is moving relative to the system being observed measures a time interval longer than the proper time.

Conceptual Questions

(a) Does motion affect the rate of a clock as measured by an observer moving with it? (b) Does motion affect how an observer moving relative to a clock measures its rate?

To whom does the elapsed time for a process seem to be longer, an observer moving relative to the process or an observer moving with the process? Which observer measures the interval of proper time?

The observer moving with the process sees its interval of proper time, which is the shortest seen by any observer.

(a) How could you travel far into the future of Earth without aging significantly? (b) Could this method also allow you to travel into the past?

a. 1.0328; b. 1.15

A neutron lives 900 s when at rest relative to an observer. How fast is the neutron moving relative to an observer who measures its life span to be 2065 s?

Time Dilation Copyright © by Samuel J. Ling; Jeff Sanny; and William Moebs is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Time Dilation

Claimed By Frank Hutchison Spring 2022

Note: This article is regarding time dilation due to relative velocity (special relativity). Time dilation is a phenomenon that is exemplified by an apparent disparity in the passage of time within the context of multiple frames of reference.

• 1.1 Inertial Reference Frames
• 2.1 A Mathematical Model
• 3.2 Difficult
• 4.1 Train Simultaneity
• 5 Twin Paradox
• 6 Length Contraction
• 7 Connectedness
• 9.1 Further reading
• 9.2 External links
• 10 References

Before Einstein, the best equations to model the interactions between objects were from Isaac Newton. The concept is known as classical mechanics. For everyday occurrences, such as an apple falling from a tree, Newton’s equations give accurate predictions. The best application of classical mechanics involved the motion of planets. Newton theorized that the Earth was pulling the moon and other objects (like the apple) towards itself. The moon balanced this force of gravity through its inertia. This logic was then applied to planets orbiting the Sun.

Inertial Reference Frames

An important thing to note about observing objects is that a reference point has to made. When a person is sitting, he is usually said to not be moving. However, this is misleading. In reality, the person is moving at the same speed as the Earth is rotating. The person is also moving at the speed the Earth is revolving around the Sun. The reason we don’t feel it is because the rotating and revolving speeds are constant. So, an inertial reference is when we pick something (an example would be the Earth) and assume it is not moving. We then compare other objects to that frame. This then means that velocity is relative or depends on the frame chosen. Example: There is a person standing still (relative to the Earth), a person driving a car at a constant speed, and a person walking. If the reference frame is from the person standing still, the person walking is moving at 5mph and the person in the car is going 20mph. From the reference frame of the person walking, the stationary person is moving at -5mph and the person in the car is going 15mph. For more information, watch this video. [1] Newton’s laws describe motion well in inertial reference frames like ours. However, they break down at high speeds. Another issue is that time is not the same in every inertial frame. Einstein’s Theory of Special Relativity fills in these gaps.

The Main Idea

Time dilation is best understood to be entirely based on reference frames. All effects or observed effects of time dilation are dependent on the observer's particular frame of reference. For example (as the concept of time dilation relates to special relativity), a pilot travelling in a rocket will observe no change in his own situation, despite the fact that, to an outside observer who is "not moving," the pilot and his instruments will be subject to a great deal of time dilation due to the high velocity disparity between the rocket and the observer.

A Mathematical Model

Time dilation in a special relativistic context can be modeled simply with the formula:

where [math]\displaystyle{ \Delta t }[/math] defines the elapsed time between two events which occur at the same location for one particular observer in his or her frame of reference, [math]\displaystyle{ \Delta t' }[/math] defines a second measured elapsed time between the same two events but by a second particular observer that is moving with a specific velocity of [math]\displaystyle{ v }[/math] with respect to the first observer. In this context, [math]\displaystyle{ c }[/math] refers to the speed of light. For everyday events, the velocity of the observed objects is so small compared to light (300 million meters/second) that the time dilation is negligible. This is not the case for particles moving near the speed of light. Say a particle was moving at 99% the speed of light for one second in our reference frame. In the particles reference frame, it travels longer.

This gets more extreme the closer the speed is to light. Let’s use the same scenario as above but instead the particle is moving at 99.99% the speed of light.

These changes in time depending on the reference frame can have startling implications. Below are two examples along with two paradoxes.

Imagine a flight from Cleveland to Atlanta. It would seem obvious that the distance covered by a plane that undertakes this journey is identical to a plane that flies from Atlanta to Cleveland. However, it must be considered which plane is actually moving relative to our frame of reference. In order to understand more complicated aspects of time dilation, simple facts about referential velocities are important to learn.

Imagine spaceship one is moving at a uniform speed from point A to point B. Spaceship one has an on-board atomic clock that measures time accurately to the nanosecond. Now, imagine a second, identical spaceship (spaceship two) with an identical atomic clock moving at the same speed but this time heading from point B to point A. At the instance that the spaceships pass by one another on their respective routes, the pilot of spaceship one looks into the cockpit of spaceship two and notices that the atomic clock appears to be ticking slower in comparison to his own atomic clock, which seems to operate normally. Compare this to the viewpoint of the pilot of spaceship two, who sees his clock as operating normally whereas the clock in spaceship one appears to be slower.

The reasoning behind the apparent disparity involves the differing frames of reference of the two pilots. But what happens if the two pilots later decide to meet up at the restaurant at the end of the universe? Which one will be older? To answer this question simply, neither will be "older" than one another, but in comparison to a person who had been standing still on earth during the course of the two pilots' travels, the pilots will have aged somewhat slower.

Andromeda Paradox/Simultaneity

In this scenario, Bob is stationary while Alice is running. After they exchange greetings, Alice mentions that an armada from the Andromeda Galaxy has left for Earth. Bob responds by saying they haven’t. Time dilation makes it possible for a circumstance to happen in one frame while the other the frame hasn’t experienced it yet. Put another way, simultaneity has been broken.

Train Simultaneity

Let’s look at another example. There’s a train that can go close to the speed of light. A person decides to board it, while their friend remains at the station. The train then leaves at a constant speed close to light. Suppose the person on the train fires to two lasers, one towards the front of the train, and one towards the back of the train. The person on the train would see the light from the lasers hit the front and back at the same time. Here is a simulation of what the person on the train sees. [2] It is different than what the person on the station would see. He would see light hit the back of the train before the front of the train. Here is a simulation of what the person on the station would see. [3] Why does this happen? It has to do with the constant speed of light. The distance an object travels is given by d=vt, and in this case light travels to the person’s eye at speed c, so d1=ct. Remember, the train has a specific length, L, so the distance from the front of the train, d2, will be different (and longer) than d1. Light remains constant, so time has to increase to account for the different distance, or d2=ct'. In this example we are assuming the train is moving towards the right. If it moved to the left, the person at the station would see what was before the front side of the train get struck by lightning first. For more detail on this topic, watch this video: [4]

Twin Paradox

There are two twins, Christian and Alfred. Christian leaves on a rocket ship to Barnard’s star, approximately six light years away. The ship will travel a constant speed at 80% the speed of light. Both brothers start stop watches at the same time Christian leaves. In Alfred’s perspective, he ages 15 years, 7.5 years for the journey to the star and 7.5 years for the journey back to Earth. However, Christian’s perspective is different, and we can calculate the amount of time he aged.

So, Christian aged 9 years while Alfred aged 15 years. The next question that needs to be answered is, why does Alfred age more than Christian? From Christian’s perspective, Alfred was the moving away and back towards him since Christian was moving at a constant speed. The answer is that Christian was actually in two reference frames, one heading towards the star, and one heading back towards Earth. Alfred was always in one reference frame on Earth.

Length Contraction

There’s another effect that can be witnessed when reference frames travel at speeds close to the speed of light. It has to do with the length of the object. The first thing that goes into the equation is the value of the proper length. Proper length (Lo) is the distance between two objects from the perspective of someone who is not moving towards or away from both objects. It is included in the equation below.

Here is an example to better understand the concept. Suppose a person observes a particle moving at 95% the speed of light for 3 seconds. What is the length travelled in the particle’s frame? Start by determining the distance in our reference frame.

Next, determine the length in the particle’s frame.

Alternatively, this problem could be solved using time dilation.

Comparing the two distances, we see that because the particle is moving at a much greater velocity compared to us, it appears to have travelled a lot farther than it has in its reference frame.

Connectedness

In regards to my particular major, nuclear engineering, this topic does not have a specific connection. However, the concept of time dilation is one that must be taken into special consideration in the field of aerospace engineering, specifically when designing and engineering methods for deep-space flights. Since the effects of time dilation will result in any extremely high-velocity travel, any human subjects will age at a rate much more slowly than scientists and engineers on earth working on deep-space missions. In the future, this phenomenon indeed presents a unique obstacle for exploration efforts.

In 1909, Gilbert Lewis used a model of two "light clocks," each of which moved with relative velocities, to describe a theory of time dilation. The clocks operated by bouncing a "signal light" back and forth between two mirrors; within each clock, the mirrors were parallel to each other as well as to the direction of the clock's motion. It was theorized by Lewis that an observer at the reference frame of the first clock would see the second clock as operating "slower."

• Einstein's Theory of Special Relativity

Provides context for the theories that lead up to time dilation.

• Einstein's Theory of General Relativity

Offers an alternate perspective, specifically in the context of how time dilation affects observable events.

Further reading

Hazla, Miroslav, "Dilation of Time and Space: An Examination of the True Nature of Spacetime."

Pabisch, Roland, "Derivation of the time dilatation effect from fundamental properties of photons."

External links

http://science.howstuffworks.com/science-vs-myth/everyday-myths/relativity10.htm

https://www.fourmilab.ch/cship/timedial.html

http://www.emc2-explained.info/Time-Dilation/#.VmHN4vmrTjY

https://science.howstuffworks.com/innovation/scientific-experiments/newton-law-of-motion5.htm

https://medium.com/mathadam/the-andromeda-paradox-b4bb30a0e372

https://www.youtube.com/watch?v=GgvajuvSpF4

https://www.space.com/18964-the-nearest-stars-to-earth-infographic.html

https://nigerianscholars.com/tutorials/special-relativity/proper-length/

• Interactions

Navigation menu

Time Dilation Calculator

What is time dilation — time is relative, the time dilation formula.

The time dilation calculator gives you a better idea of the time behavior according to special relativity.

Einstein's relativity theory has shown that time is relative. Time perceived by one observer in its frame of reference differs from that of another observer in another inertial frame. Please keep reading to find out what time dilation is and what happens to it when we approach to the speed of light ⌛

One of Einstein's special relativity theory's implications is that time is not absolute but rather relative.

The example of two inertial observers A and B, each carrying a clock, is frequently used to illustrate this relativeness aspect of time. If observer A remains stationary while observer B travels relative to A, B will see A's clocks moving slower than theirs. Similarly, A will perceive B's clock to be going slower — Observers perceive that a clock moves slower when it moves relative to them.

This effect of the time slowing down is known as time dilation. And the faster the relative velocity between observers, the greater the time dilation is, becoming more evident when speed approaches values in the order of magnitude of the speed of light. In special relativity, the principle that the speed of light is constant for every observer is essential, as it explains why time has to dilate in order for the speed of light to remain the same regardless of the observer's own motion.

Another common thought exercise used to explain time dilation is the twin paradox. In this imaginary situation, one twin travels into space in a high-speed rocket while his sibling stays on Earth. The astronaut-twin moves at a speed closer to the speed of light and, after some years, returns to Earth. Once back on Earth, the astronaut-twin finds his Earth-twin has aged lots more than he has.

You may wonder what the paradox is in this situation. The paradox arises when we consider the astronaut-twin to be the one that's stationary and the Earth-twin the one that's relatively moving. In this case, the Earth-twin would be younger than the astronaut. So, why is it stated that it's Earth-twin who has aged more? The reason for this is that these situations are not symmetrical. The astronaut-twin is undergoing a non-inertial movement (accelerating and decelerating during his journey), while his brother is moving in a non-accelerated relative motion.

To learn more about relativity and the relationship between mass and energy, visit the e = mc² calculator !

💡 Did you know there's another form of time dilation known as gravitational time dilation ?

Time dilation is determined as the difference of time perceived by the moving observer and the stationary observer Δ t ′ \Delta t' Δ t ′ . The time dilation formula based on special relativity is:

• Δ t ′ \Delta t' Δ t ′ — Time that has passed as measured by the traveling observer (relative time);
• γ \gamma γ — Lorentz factor, 1 − v 2 / c 2 {\sqrt{1- v^2/c^2}} 1 − v 2 / c 2 ​ ;
• Δ t \Delta t Δ t — Time that has passed as measured by a stationary observer;
• v v v — Speed of the traveling observer; and
• c c c — Speed of light (299,792,458 m/s).

You can learn more about the Lorentz factor of a moving object with the Lorentz factor calculator.

This is the expression used by the time dilation calculator ⌛ Notice that for this time difference to be evident, the speed v v v must be at least in the order of magnitude of the speed of light to obtain any substantial difference in times observed by moving and stationary observers.

Nevertheless, the time dilation effect has been proved at speeds many orders of magnitude lower than the speed of light. This is the case of an experiment conducted in 1971 using three sets of atomic clocks. One of them remained on Earth while the others flew aboard two different airplanes. The results showed a difference in times elapsed by all sets of clocks.

💡 Give the time dilation calculator a try! What happens to time dilation values when you enter a speed of 0.001   c 0.001 \ c 0.001   c and then 0.9   c 0.9 \ c 0.9   c ?

Relativistic kinetic energy

Schwarzschild radius, space travel.

• Astrophysics ( 17 )
• Atmospheric thermodynamics ( 11 )
• Continuum mechanics ( 21 )
• Conversion ( 15 )
• Dynamics ( 20 )
• Electrical energy ( 12 )
• Electromagnetism ( 18 )
• Electronics ( 34 )
• Fluid mechanics ( 29 )
• Kinematics ( 21 )
• Machines and mechanisms ( 20 )
• Math and statistics ( 34 )
• Optics ( 15 )
• Physical chemistry ( 15 )
• Quantum mechanics ( 14 )
• Relativity ( 9 )
• Rotational and periodic motion ( 17 )
• Thermodynamics ( 31 )
• Waves ( 14 )
• Other ( 33 )

This is a derivation of the time dilation formula. This will be covered in detail in class, but here it is just in case it goes by too fast. Refer to Fig. 1.

A clock is made by sending a pulse of light toward a mirror at a distance L and back to a receiver. Each "tick" is a round-trip to the mirror. The clock is shown at rest in the "Lab" frame in Fig. 1a, or any time it is in its own rest frame. Consequently, it also represents the clock at rest in rocket#1. Figure 1b is the way the clock looks in the lab when the clock is at rest in rocket#1, which is moving to the right with velocity v .

Actually, our clock "ticks" once every round-trip of the light pulse. So, we should use ct=2L, etc. But since both legs of the round-trip are the same, we'll just use the one-way times for simplicity.

Some notation :

t = time for light to reach the mirror in the lab for a clock at rest in Rocket #1 (Fig. 1b) t' = time for light to reach the mirror in Rocket#1 in its own rest frame (Fig. 1a) L = distance to mirror

So, the times and distances are related as follows: L = ct' L 2 + v 2 *t 2 = c 2 *t 2 (Pythagorean theorem)

Eliminate L from the equations: c 2 *t' 2 = c 2 *t 2 - v 2 *t 2 t' = t*√(1-v 2 /c 2 )

Since √(1-v 2 /c 2 )<1, the clock at rest in rocket#1 appears slow to observers in the lab.

Go back to Fig. 1c. Rocket#2 is moving with velocity v to the left . Those clocks would also appear slow to observers in the lab. But, it is also the way a clock at rest in the lab appears in rocket#1. So, lab clocks also appear slow to observers in the rockets. Relativity is symmetrical!

Lorentz Contraction

This is a derivation of the Lorentz-contraction formula. We will go over the ideas in class, but the algebra is a bit gruesome. So, I'm putting that part here. Refer to Fig. 2.

As with the time dilation example, imagine a pulse of light reflects from a mirror back to a receiver. Light will be the "yardstick" used to measure the length of an object in the lab and rocket frames.

L' = length of stick in the "rocket" L = length of stick in the "lab" t1 = travel time of light pulse to the end of the stick (lab) t2 = travel time of light pulse back from the end of the stick (lab) t = t1+t2 = total travel time in the lab t' = total travel time in the rocket v = speed of rocket in the lab frame

In the lab: L + v*t1 = c*t1 L - v*t2 = c*t2 t = t1 + t2 = (2L/c)/(1-v 2 /c 2 )

In the rocket: 2L' = c*t' t' = 2L'/c

We know from the time dilation formula that t' = t*√(1-v 2 /c 2 )

So, 2L'/c = (2L/c)/√(1-v 2 /c 2 ) L' = L/√(1-v 2 /c 2 ) L = L'*√(1-v 2 /c 2 )

The stick appears shorter in the lab frame since √(1-v 2 /c 2 )<1.

Return to the Syllabus .

This page is copyright ©1997-2000 by G. G. Lombardi. All rights reserved.

Special Relativity

Simultaneity and time dilation, learning objectives.

By the end of this section, you will be able to:

• Describe simultaneity.
• Describe time dilation.
• Calculate γ.
• Compare proper time and the observer’s measured time.
• Explain why the twin paradox is a false paradox.

Figure 1. Elapsed time for a foot race is the same for all observers, but at relativistic speeds, elapsed time depends on the relative motion of the observer and the event that is observed. (credit: Jason Edward Scott Bain, Flickr)

Do time intervals depend on who observes them? Intuitively, we expect the time for a process, such as the elapsed time for a foot race, to be the same for all observers. Our experience has been that disagreements over elapsed time have to do with the accuracy of measuring time. When we carefully consider just how time is measured, however, we will find that elapsed time depends on the relative motion of an observer with respect to the process being measured.

Simultaneity

Consider how we measure elapsed time. If we use a stopwatch, for example, how do we know when to start and stop the watch? One method is to use the arrival of light from the event, such as observing a light turning green to start a drag race. The timing will be more accurate if some sort of electronic detection is used, avoiding human reaction times and other complications.

Now suppose we use this method to measure the time interval between two flashes of light produced by flash lamps. (See Figure 2.) Two flash lamps with observer A midway between them are on a rail car that moves to the right relative to observer B. The light flashes are emitted just as A passes B, so that both A and B are equidistant from the lamps when the light is emitted. Observer B measures the time interval between the arrival of the light flashes. According to postulate 2, the speed of light is not affected by the motion of the lamps relative to B. Therefore, light travels equal distances to him at equal speeds. Thus observer B measures the flashes to be simultaneous.

Figure 2. Observer B measures the elapsed time between the arrival of light flashes as described in the text. Observer A moves with the lamps on a rail car. Observer B receives the light flashes simultaneously, but he notes that observer A receives the flash from the right first. B observes the flashes to be simultaneous to him but not to A. Simultaneity is not absolute.

Now consider what observer B sees happen to observer A. She receives the light from the right first, because she has moved towards that flash lamp, lessening the distance the light must travel and reducing the time it takes to get to her. Light travels at speed c relative to both observers, but observer B remains equidistant between the points where the flashes were emitted, while A gets closer to the emission point on the right. From observer B’s point of view, then, there is a time interval between the arrival of the flashes to observer A. Observer B measures the flashes to be simultaneous relative to him but not relative to A. Here a relative velocity between observers affects whether two events are observed to be simultaneous. Simultaneity is not absolute .

This illustrates the power of clear thinking. We might have guessed incorrectly that if light is emitted simultaneously, then two observers halfway between the sources would see the flashes simultaneously. But careful analysis shows this not to be the case. Einstein was brilliant at this type of thought experiment (in German, “Gedankenexperiment”). He very carefully considered how an observation is made and disregarded what might seem obvious. The validity of thought experiments, of course, is determined by actual observation. The genius of Einstein is evidenced by the fact that experiments have repeatedly confirmed his theory of relativity.

In summary: Two events are defined to be simultaneous if an observer measures them as occurring at the same time (such as by receiving light from the events). Two events are not necessarily simultaneous to all observers.

Time Dilation

The consideration of the measurement of elapsed time and simultaneity leads to an important relativistic effect.

• Time dilation is the phenomenon of time passing slower for an observer who is moving relative to another observer.

Suppose, for example, an astronaut measures the time it takes for light to cross her ship, bounce off a mirror, and return. (See Figure 3.) How does the elapsed time the astronaut measures compare with the elapsed time measured for the same event by a person on the Earth? Asking this question (another thought experiment) produces a profound result. We find that the elapsed time for a process depends on who is measuring it. In this case, the time measured by the astronaut is smaller than the time measured by the Earth-bound observer. The passage of time is different for the observers because the distance the light travels in the astronaut’s frame is smaller than in the Earth-bound frame. Light travels at the same speed in each frame, and so it will take longer to travel the greater distance in the Earth-bound frame.

Figure 3. (a) An astronaut measures the time Δt0 for light to cross her ship using an electronic timer. Light travels a distance 2D in the astronaut’s frame. (b) A person on the Earth sees the light follow the longer path 2s and take a longer time Δt. (c) These triangles are used to find the relationship between the two distances 2D and 2s.

To quantitatively verify that time depends on the observer, consider the paths followed by light as seen by each observer. (See Figure 3c.) The astronaut sees the light travel straight across and back for a total distance of 2 D , twice the width of her ship. The Earth-bound observer sees the light travel a total distance 2 s . Since the ship is moving at speed v to the right relative to the Earth, light moving to the right hits the mirror in this frame. Light travels at a speed c in both frames, and because time is the distance divided by speed, the time measured by the astronaut is [latex]\Delta{t}_0=\frac{2D}{c}\\[/latex].

This time has a separate name to distinguish it from the time measured by the Earth-bound observer.

Proper Time

Proper time  Δ t 0 is the time measured by an observer at rest relative to the event being observed.

In the case of the astronaut observe the reflecting light, the astronaut measures proper time. The time measured by the Earth-bound observer is [latex]\Delta{t}=\frac{2d}{c}\\[/latex].

To find the relationship between Δ t 0 and Δ t , consider the triangles formed by D and s . (See Figure 3c.) The third side of these similar triangles is L , the distance the astronaut moves as the light goes across her ship. In the frame of the Earth-bound observer, [latex]L=\frac{v\Delta{t}}{2}\\[/latex].

Using the Pythagorean Theorem, the distance s is found to be

[latex]\displaystyle{s}=\sqrt{D^2+\left(\frac{v\Delta{t}}{2}\right)^2}\\[/latex]

Substituting s into the expression for the time interval Δ t gives

[latex]\displaystyle\Delta{t}=\frac{2s}{c}=\frac{2\sqrt{D^2+\left(\frac{v\Delta{t}}{2}\right)^2}}{c}\\[/latex]

We square this equation, which yields

[latex]\displaystyle\left(\Delta{t}\right)^2=\frac{4\left(D^2+\frac{v^2\left(\Delta{t}\right)^2}{4}\right)}{c^2}=\frac{4D^2}{c^2}+\frac{v^2}{c^2}\left(\Delta{t}\right)^2\\[/latex]

Note that if we square the first expression we had for Δ t 0 , we get [latex]\left(\Delta{t}_0\right)^2=\frac{4D^2}{c^2}\\[/latex]. This term appears in the preceding equation, giving us a means to relate the two time intervals. Thus,

[latex]\displaystyle\left(\Delta{t}\right)^2=\left(\Delta{t}_0\right)^2+\frac{v^2}{c^2}\left(\Delta{t}\right)^2\\[/latex]

Gathering terms, we solve for Δ t :

[latex]\displaystyle\left(\Delta{t}\right)^2\left(1-\frac{v^2}{c^2}\right)=\left(\Delta{t}_0\right)^2\\[/latex]

[latex]\displaystyle\left(\Delta{t}\right)^2=\frac{\left(\Delta{t}_0\right)^2}{1-\frac{v^2}{c^2}}\\[/latex]

Taking the square root yields an important relationship between elapsed times:

[latex]\displaystyle\Delta{t}=\frac{\Delta{t}_0}{\sqrt{1-\frac{v^2}{c^2}}}=\gamma\Delta{t}_0\\[/latex]

[latex]\displaystyle\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\\[/latex]

This equation for Δ t is truly remarkable. First, as contended, elapsed time is not the same for different observers moving relative to one another, even though both are in inertial frames. Proper time Δ t 0 measured by an observer, like the astronaut moving with the apparatus, is smaller than time measured by other observers. Since those other observers measure a longer time Δ t , the effect is called time dilation. The Earth-bound observer sees time dilate (get longer) for a system moving relative to the Earth. Alternatively, according to the Earth-bound observer, time slows in the moving frame, since less time passes there. All clocks moving relative to an observer, including biological clocks such as aging, are observed to run slow compared with a clock stationary relative to the observer.

Note that if the relative velocity is much less than the speed of light ( v  <<  c ), then [latex]\frac{v^2}{c^2}\\[/latex] is extremely small, and the elapsed times Δ t and Δ t 0 are nearly equal. At low velocities, modern relativity approaches classical physics—our everyday experiences have very small relativistic effects.

The equation Δ t  = γ Δ t 0 also implies that relative velocity cannot exceed the speed of light. As v approaches c , Δ t approaches infinity. This would imply that time in the astronaut’s frame stops at the speed of light. If v exceeded c , then we would be taking the square root of a negative number, producing an imaginary value for Δ t .

There is considerable experimental evidence that the equation Δ t  =  γ Δ t 0 is correct. One example is found in cosmic ray particles that continuously rain down on the Earth from deep space. Some collisions of these particles with nuclei in the upper atmosphere result in short-lived particles called muons. The half-life (amount of time for half of a material to decay) of a muon is 1.52 μ s when it is at rest relative to the observer who measures the half-life. This is the proper time Δ t 0 . Muons produced by cosmic ray particles have a range of velocities, with some moving near the speed of light. It has been found that the muon’s half-life as measured by an Earth-bound observer (Δ t ) varies with velocity exactly as predicted by the equation Δ t  =  γ Δ t 0 . The faster the muon moves, the longer it lives. We on the Earth see the muon’s half-life time dilated—as viewed from our frame, the muon decays more slowly than it does when at rest relative to us.

Example 1. Calculating [latex]\Delta{t}\\[/latex] for a Relativistic Event: How Long Does a Speedy Muon Live?

Suppose a cosmic ray colliding with a nucleus in the Earth’s upper atmosphere produces a muon that has a velocity v  = 0.950 c . The muon then travels at constant velocity and lives 1.52 μ s as measured in the muon’s frame of reference. (You can imagine this as the muon’s internal clock.) How long does the muon live as measured by an Earth-bound observer? (See Figure 4.)

Figure 4. A muon in the Earth’s atmosphere lives longer as measured by an Earth-bound observer than measured by the muon’s internal clock.

A clock moving with the system being measured observes the proper time, so the time we are given is Δ t 0   = 1.52 μ s. The Earth-bound observer measures Δ t as given by the equation Δ t  =   γ Δ t 0 . Since we know the velocity, the calculation is straightforward.

Identify the knowns:  v  = 0.950 c , Δ t 0  = 1.52 μ s

Identify the unknown: Δ t

Choose the appropriate equation. Use Δ t  =  γ Δ t 0 , where [latex]\displaystyle\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\\[/latex].

Plug the knowns into the equation.

First find γ .

[latex]\begin{array}{lll}\gamma&=&\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\\\text{ }&=&\frac{1}{\sqrt{1-\frac{\left(0.950c\right)^2}{c^2}}}\\\text{ }&=&\frac{1}{\sqrt{1-\left(0.950\right)^2}}\\\text{ }&=&3.20\end{array}\\[/latex]

Use the calculated value of γ to determine Δ t .

[latex]\begin{array}{lll}\Delta{t}&=&\gamma\Delta{t}_0\\\text{ }&=&\left(3.20\right)\left(1.52\mu\text{s}\right)\\\text{ }&=&4.87\mu\text{s}\end{array}\\[/latex]

One implication of this example is that since γ  = 3.20 at 95.0% of the speed of light ( v  = 0.950 c ), the relativistic effects are significant. The two time intervals differ by this factor of 3.20, where classically they would be the same. Something moving at 0.950 c is said to be highly relativistic.

Another implication of the preceding example is that everything an astronaut does when moving at 95.0% of the speed of light relative to the Earth takes 3.20 times longer when observed from the Earth. Does the astronaut sense this? Only if she looks outside her spaceship. All methods of measuring time in her frame will be affected by the same factor of 3.20. This includes her wristwatch, heart rate, cell metabolism rate, nerve impulse rate, and so on. She will have no way of telling, since all of her clocks will agree with one another because their relative velocities are zero. Motion is relative, not absolute. But what if she does look out the window?

Real-World Connections

It may seem that special relativity has little effect on your life, but it is probably more important than you realize. One of the most common effects is through the Global Positioning System (GPS). Emergency vehicles, package delivery services, electronic maps, and communications devices are just a few of the common uses of GPS, and the GPS system could not work without taking into account relativistic effects. GPS satellites rely on precise time measurements to communicate. The signals travel at relativistic speeds. Without corrections for time dilation, the satellites could not communicate, and the GPS system would fail within minutes.

The Twin Paradox

An intriguing consequence of time dilation is that a space traveler moving at a high velocity relative to the Earth would age less than her Earth-bound twin. Imagine the astronaut moving at such a velocity that γ = 30.0, as in Figure 5. A trip that takes 2.00 years in her frame would take 60.0 years in her Earth-bound twin’s frame. Suppose the astronaut traveled 1.00 year to another star system. She briefly explored the area, and then traveled 1.00 year back. If the astronaut was 40 years old when she left, she would be 42 upon her return. Everything on the Earth, however, would have aged 60.0 years. Her twin, if still alive, would be 100 years old.

The situation would seem different to the astronaut. Because motion is relative, the spaceship would seem to be stationary and the Earth would appear to move. (This is the sensation you have when flying in a jet.) If the astronaut looks out the window of the spaceship, she will see time slow down on the Earth by a factor of γ  = 30.0. To her, the Earth-bound sister will have aged only 2/30 (1/15) of a year, while she aged 2.00 years. The two sisters cannot both be correct.

Figure 5. The twin paradox asks why the traveling twin ages less than the Earth-bound twin. That is the prediction we obtain if we consider the Earth-bound twin’s frame. In the astronaut’s frame, however, the Earth is moving and time runs slower there. Who is correct?

As with all paradoxes, the premise is faulty and leads to contradictory conclusions. In fact, the astronaut’s motion is significantly different from that of the Earth-bound twin. The astronaut accelerates to a high velocity and then decelerates to view the star system. To return to the Earth, she again accelerates and decelerates. The Earth-bound twin does not experience these accelerations. So the situation is not symmetric, and it is not correct to claim that the astronaut will observe the same effects as her Earth-bound twin. If you use special relativity to examine the twin paradox, you must keep in mind that the theory is expressly based on inertial frames, which by definition are not accelerated or rotating. Einstein developed general relativity to deal with accelerated frames and with gravity, a prime source of acceleration. You can also use general relativity to address the twin paradox and, according to general relativity, the astronaut will age less. Some important conceptual aspects of general relativity are discussed in General Relativity and Quantum Gravity of this course.

In 1971, American physicists Joseph Hafele and Richard Keating verified time dilation at low relative velocities by flying extremely accurate atomic clocks around the Earth on commercial aircraft. They measured elapsed time to an accuracy of a few nanoseconds and compared it with the time measured by clocks left behind. Hafele and Keating’s results were within experimental uncertainties of the predictions of relativity. Both special and general relativity had to be taken into account, since gravity and accelerations were involved as well as relative motion.

Check Your Understanding

1. What is γ if v  = 0.650 c ?

[latex]\displaystyle\gamma=\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{1}{\sqrt{1-\frac{\left(0.650c\right)^2}{c^2}}}=1.32\\[/latex]

2. A particle travels at 1.90 × 10 8 m/s and lives 2.10 × 10 −8 s when at rest relative to an observer. How long does the particle live as viewed in the laboratory?

[latex]\displaystyle\Delta{t}=\frac{\Delta{t}}{\sqrt{1-\frac{v^2}{c^2}}}=\frac{2.10\times10^{-8}\text{ s}}{\sqrt{1-\frac{\left(1.90\times10^8\text{ m/s}\right)^2}{\left(3.00\times10^8\text{ m/s}\right)^2}}}=2.71\times10^{-8}\text{ s}\\[/latex]

Section Summary

• Two events are defined to be simultaneous if an observer measures them as occurring at the same time. They are not necessarily simultaneous to all observers—simultaneity is not absolute.
• Observers moving at a relative velocity v  do not measure the same elapsed time for an event. Proper time Δ t 0  is the time measured by an observer at rest relative to the event being observed. Proper time is related to the time Δ t measured by an Earth-bound observer by the equation [latex]\displaystyle\Delta t=\frac{{\Delta t}_{0}}{\sqrt{1-\frac{{v}^{2}}{{c}^{2}}}}={\gamma \Delta t}_{0}\\[/latex], where [latex]\displaystyle\gamma =\frac{1}{\sqrt{1-\frac{{v}^{2}}{{c}^{2}}}}\\[/latex].
• The equation relating proper time and time measured by an Earth-bound observer implies that relative velocity cannot exceed the speed of light.
• The twin paradox asks why a twin traveling at a relativistic speed away and then back towards the Earth ages less than the Earth-bound twin. The premise to the paradox is faulty because the traveling twin is accelerating. Special relativity does not apply to accelerating frames of reference.
• Time dilation is usually negligible at low relative velocities, but it does occur, and it has been verified by experiment.

Conceptual Questions

• Does motion affect the rate of a clock as measured by an observer moving with it? Does motion affect how an observer moving relative to a clock measures its rate?
• To whom does the elapsed time for a process seem to be longer, an observer moving relative to the process or an observer moving with the process? Which observer measures proper time?
• How could you travel far into the future without aging significantly? Could this method also allow you to travel into the past?

Problems & Exercises

• (a) What is γ if v  = 0.250 c ? (b) If v  = 0.500 c ?
• (a) What is  γ if v  = 0.100 c ? (b) If v  = 0.900 c ?
• Particles called π-mesons are produced by accelerator beams. If these particles travel at 2.70 × 10 8 m/s and live 2.60 × 10 −8 s when at rest relative to an observer, how long do they live as viewed in the laboratory?
• Suppose a particle called a kaon is created by cosmic radiation striking the atmosphere. It moves by you at 0.980 c , and it lives 1.24 × 10 −8 s when at rest relative to an observer. How long does it live as you observe it?
• A neutral π-meson is a particle that can be created by accelerator beams. If one such particle lives 1.40 × 10 −16 s as measured in the laboratory, and 0.840 × 10 −16 s when at rest relative to an observer, what is its velocity relative to the laboratory?
• A neutron lives 900 s when at rest relative to an observer. How fast is the neutron moving relative to an observer who measures its life span to be 2065 s?
• If relativistic effects are to be less than 1%, then γ must be less than 1.01. At what relative velocity is γ = 1.01?
• If relativistic effects are to be less than 3%, then  γ must be less than 1.03. At what relative velocity is  γ = 1.03?
• (a) At what relative velocity is  γ = 1.50? (b) At what relative velocity is  γ = 100?
• (a) At what relative velocity is γ = 2.00? (b) At what relative velocity is  γ = 10.0?
• Unreasonable Results.  (a) Find the value of  γ for the following situation. An Earth-bound observer measures 23.9 h to have passed while signals from a high-velocity space probe indicate that 24.0 h have passed on board. (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?

time dilation:  the phenomenon of time passing slower to an observer who is moving relative to another observer

proper time: Δ t 0 . the time measured by an observer at rest relative to the event being observed:

[latex]\displaystyle\Delta t=\frac{{\Delta t}_{0}}{\sqrt{1-\frac{{v}^{2}}{{c}^{2}}}}={\gamma \Delta t}_{0}\\[/latex], where [latex]\displaystyle\gamma =\frac{1}{\sqrt{1-\frac{{v}^{2}}{{c}^{2}}}}\\[/latex]

twin paradox:  this asks why a twin traveling at a relativistic speed away and then back towards the Earth ages less than the Earth-bound twin. The premise to the paradox is faulty because the traveling twin is accelerating, and special relativity does not apply to accelerating frames of reference

Selected Solutions to Problems & Exercises

1. (a) 1.0328; (b) 1.15

3. 5.96 × 10 −8 s

9. (a) 0.745 c ; (b) 0.99995 c  (to five digits to show effect)

11. (a) 0.996; (b)  γ cannot be less than 1; (c) Assumption that time is longer in moving ship is unreasonable.

• College Physics. Authored by : OpenStax College. Located at : http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a/College_Physics . License : CC BY: Attribution . License Terms : Located at License

This topic fits quite well into a number of mathematical topics – from graphing, to real life uses of equations, to standard form and unit conversions. It also challenges our notion of time as we usually experience it and therefore leads onto some interesting questions about the nature of reality. Below we can see the time dilation graph:

which clearly shows that for low speeds there is very little time dilation, but when we start getting to within 90% of the speed of light, that there is a very significant time dilation effect. For more accuracy we can work out the exact dilation using the formula given – where v is the speed traveled, c is the speed of light, t is the time experienced in the observer’s own frame of reference (say, by looking at his watch) and t’ is the time experienced in a different, stationary time frame (say on Earth) . Putting some numbers in for real life examples:

1) A long working air steward spends a cumulative total of 5 years in the air – flying at an average speed of 900km/h. How much longer will he live (from a stationary viewpoint) compared to if he had been a bus driver?

2) Voyager 1, launched in 1977 and now currently about 1.8×10^10 km away from Earth is traveling at around 17km/s. How far does this craft travel in 1 hour? What would the time dilation be for someone onboard since 1977?

3) I built a spacecraft capable of traveling at 95% the speed of light. I said goodbye to my twin sister and hopped aboard, flew for a while before returning to Earth. If I experienced 10 years on the space craft, how much younger will I be than my twin?

Scroll to the bottom for the answers

Marcus De Sautoy also presents an interesting Horizon documentary on the speed of light, its history and the CERN experiments last year that suggested that some particles may have traveled faster than light:

There is a lot of scope for extra content on this topic – for example, looking at the distance of some stars visible in the night sky. For example, red super-giant star Belelgeuse is around 600 light years from Earth. (How many kilometres is that?) When we look at Betelgeuse we are actually looking 600 years “back in time” – so does it make sense to use time as a frame of reference for existence?

1) Convert 900km/h into km/s = 0.25km/s. Now substitute this value into the equation, along with the speed of light at 300,000km/s….and even using Google’s computer calculator we get a difference so negligible that the denominator rounds to 1.

2) With units already in km/s we substitute the values in – and using a powerful calculator find that denominator is 0.99999999839. Therefore someone traveling on the ship for what their watch recorded as 35 years would actually have been recorded as leaving Earth 35.0000000562 years ago. Which is about 1.78seconds! So still not much effect.

3) This time we get a denominator of 0.3122498999 and so the time experienced by my twin will be 32 years. In effect my sister will have aged 22 years more than me on my return. Amazing!

If you enjoyed this topic you might also like:

Michio Kaku – Universe in a Nutshell

Champagne Supernovas and the Birth of the Universe – some amazing pictures from space.

Essential resources for IB students:

1) Exploration Guides  and Paper 3 Resources

I’ve put together four comprehensive pdf guides to help students prepare for their exploration coursework and Paper 3 investigations. The exploration guides talk through the marking criteria, common student mistakes, excellent ideas for explorations, technology advice, modeling methods and a variety of statistical techniques with detailed explanations. I’ve also made 17 full investigation questions which are also excellent starting points for explorations.  The Exploration Guides can be downloaded here  and the Paper 3 Questions can be downloaded here .

Share this:

Leave a reply cancel reply.

Powered by WordPress.com .

Discover more from IB Maths Resources from Intermathematics

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

A beginner's guide to time travel

Learn exactly how Einstein's theory of relativity works, and discover how there's nothing in science that says time travel is impossible.

Everyone can travel in time . You do it whether you want to or not, at a steady rate of one second per second. You may think there's no similarity to traveling in one of the three spatial dimensions at, say, one foot per second. But according to Einstein 's theory of relativity , we live in a four-dimensional continuum — space-time — in which space and time are interchangeable.

Einstein found that the faster you move through space, the slower you move through time — you age more slowly, in other words. One of the key ideas in relativity is that nothing can travel faster than the speed of light — about 186,000 miles per second (300,000 kilometers per second), or one light-year per year). But you can get very close to it. If a spaceship were to fly at 99% of the speed of light, you'd see it travel a light-year of distance in just over a year of time. 

That's obvious enough, but now comes the weird part. For astronauts onboard that spaceship, the journey would take a mere seven weeks. It's a consequence of relativity called time dilation , and in effect, it means the astronauts have jumped about 10 months into the future. 

Traveling at high speed isn't the only way to produce time dilation. Einstein showed that gravitational fields produce a similar effect — even the relatively weak field here on the surface of Earth . We don't notice it, because we spend all our lives here, but more than 12,400 miles (20,000 kilometers) higher up gravity is measurably weaker— and time passes more quickly, by about 45 microseconds per day. That's more significant than you might think, because it's the altitude at which GPS satellites orbit Earth, and their clocks need to be precisely synchronized with ground-based ones for the system to work properly. 

The satellites have to compensate for time dilation effects due both to their higher altitude and their faster speed. So whenever you use the GPS feature on your smartphone or your car's satnav, there's a tiny element of time travel involved. You and the satellites are traveling into the future at very slightly different rates.

But for more dramatic effects, we need to look at much stronger gravitational fields, such as those around black holes , which can distort space-time so much that it folds back on itself. The result is a so-called wormhole, a concept that's familiar from sci-fi movies, but actually originates in Einstein's theory of relativity. In effect, a wormhole is a shortcut from one point in space-time to another. You enter one black hole, and emerge from another one somewhere else. Unfortunately, it's not as practical a means of transport as Hollywood makes it look. That's because the black hole's gravity would tear you to pieces as you approached it, but it really is possible in theory. And because we're talking about space-time, not just space, the wormhole's exit could be at an earlier time than its entrance; that means you would end up in the past rather than the future.

Trajectories in space-time that loop back into the past are given the technical name "closed timelike curves." If you search through serious academic journals, you'll find plenty of references to them — far more than you'll find to "time travel." But in effect, that's exactly what closed timelike curves are all about — time travel

This article is brought to you by  How It Works .

How It Works is the action-packed magazine that's bursting with exciting information about the latest advances in science and technology, featuring everything you need to know about how the world around you — and the universe — works.

There's another way to produce a closed timelike curve that doesn't involve anything quite so exotic as a black hole or wormhole: You just need a simple rotating cylinder made of super-dense material. This so-called Tipler cylinder is the closest that real-world physics can get to an actual, genuine time machine. But it will likely never be built in the real world, so like a wormhole, it's more of an academic curiosity than a viable engineering design.

Yet as far-fetched as these things are in practical terms, there's no fundamental scientific reason — that we currently know of — that says they are impossible. That's a thought-provoking situation, because as the physicist Michio Kaku is fond of saying, "Everything not forbidden is compulsory" (borrowed from T.H. White's novel, "The Once And Future King"). He doesn't mean time travel has to happen everywhere all the time, but Kaku is suggesting that the universe is so vast it ought to happen somewhere at least occasionally. Maybe some super-advanced civilization in another galaxy knows how to build a working time machine, or perhaps closed timelike curves can even occur naturally under certain rare conditions.

This raises problems of a different kind — not in science or engineering, but in basic logic. If time travel is allowed by the laws of physics, then it's possible to envision a whole range of paradoxical scenarios . Some of these appear so illogical that it's difficult to imagine that they could ever occur. But if they can't, what's stopping them? 

Thoughts like these prompted Stephen Hawking , who was always skeptical about the idea of time travel into the past, to come up with his "chronology protection conjecture" — the notion that some as-yet-unknown law of physics prevents closed timelike curves from happening. But that conjecture is only an educated guess, and until it is supported by hard evidence, we can come to only one conclusion: Time travel is possible.

A party for time travelers 

Hawking was skeptical about the feasibility of time travel into the past, not because he had disproved it, but because he was bothered by the logical paradoxes it created. In his chronology protection conjecture, he surmised that physicists would eventually discover a flaw in the theory of closed timelike curves that made them impossible. 

In 2009, he came up with an amusing way to test this conjecture. Hawking held a champagne party (shown in his Discovery Channel program), but he only advertised it after it had happened. His reasoning was that, if time machines eventually become practical, someone in the future might read about the party and travel back to attend it. But no one did — Hawking sat through the whole evening on his own. This doesn't prove time travel is impossible, but it does suggest that it never becomes a commonplace occurrence here on Earth.

The arrow of time 

One of the distinctive things about time is that it has a direction — from past to future. A cup of hot coffee left at room temperature always cools down; it never heats up. Your cellphone loses battery charge when you use it; it never gains charge. These are examples of entropy , essentially a measure of the amount of "useless" as opposed to "useful" energy. The entropy of a closed system always increases, and it's the key factor determining the arrow of time.

It turns out that entropy is the only thing that makes a distinction between past and future. In other branches of physics, like relativity or quantum theory, time doesn't have a preferred direction. No one knows where time's arrow comes from. It may be that it only applies to large, complex systems, in which case subatomic particles may not experience the arrow of time.

Time travel paradox 

If it's possible to travel back into the past — even theoretically — it raises a number of brain-twisting paradoxes — such as the grandfather paradox — that even scientists and philosophers find extremely perplexing.

Killing Hitler

A time traveler might decide to go back and kill him in his infancy. If they succeeded, future history books wouldn't even mention Hitler — so what motivation would the time traveler have for going back in time and killing him?

Killing your grandfather

Instead of killing a young Hitler, you might, by accident, kill one of your own ancestors when they were very young. But then you would never be born, so you couldn't travel back in time to kill them, so you would be born after all, and so on … 

A closed loop

Suppose the plans for a time machine suddenly appear from thin air on your desk. You spend a few days building it, then use it to send the plans back to your earlier self. But where did those plans originate? Nowhere — they are just looping round and round in time.

Sign up for the Live Science daily newsletter now

Get the world’s most fascinating discoveries delivered straight to your inbox.

Andrew May holds a Ph.D. in astrophysics from Manchester University, U.K. For 30 years, he worked in the academic, government and private sectors, before becoming a science writer where he has written for Fortean Times, How It Works, All About Space, BBC Science Focus, among others. He has also written a selection of books including Cosmic Impact and Astrobiology: The Search for Life Elsewhere in the Universe, published by Icon Books.

NASA's Juno probe reveals 'fire-breathing' lava lakes across Jupiter's volcanic moon Io

Rare, mystery blasts from sun can devastate the ozone layer and spike radiation levels on Earth

Searching for 'Makozilla' — the supersized mako sharks in the North Pacific

Most Popular