tour de hanoi explication

•   A la Une
•   Archives
• Technologies
•   Aéronautique
•   Transports
•   Espace
•   Energie
•   Multimédia
•   Architecture
•   Mathématiques
•   Physique
•   Astrophysique
•   Astronomie
•   Vie et Terre
•   Autres Sujets
•   Rétro
•   En ce moment
•   Codes promo Amazon FR
•   Codes promo Amazon US
•   Codes promo Banggood
•   Codes promo DHgate
•   Boutique
• Encyclopédie ✕
• Forum 💬 ✕

Tours de Hanoï - Définition

Introduction.

Le problème des tours de Hanoï est un jeu de réflexion imaginé par le mathématicien français Édouard Lucas, et consistant à déplacer des disques de diamètres différents d'une tour de « départ » à une tour d'« arrivée » en passant par une tour « intermédiaire » et ceci en un minimum de coups, tout (Le tout compris comme ensemble de ce qui existe est souvent interprété comme le monde ou...) en respectant les règles suivantes :

• on ne peut déplacer plus d'un disque (Le mot disque est employé, aussi bien en géométrie que dans la vie courante, pour désigner une...) à la fois,
• on ne peut placer un disque que sur un autre disque plus grand que lui ou sur un emplacement vide (Le vide est ordinairement défini comme l'absence de matière dans une zone spatiale.) .

On suppose que cette dernière règle est également respectée dans la configuration de départ.

Origine du problème

Le problème mathématique (Les mathématiques constituent un domaine de connaissances abstraites construites à l'aide...) des tours de Hanoï (Le problème des tours de Hanoï est un jeu de réflexion imaginé par le...) a été inventé par Édouard Lucas. Il est publié dans le tome 3 de ses Récréations mathématiques , parues à titre posthume en 1892. Il annonce que ce problème est dû à un de ses amis, N. Claus de Siam , prétendument professeur au collège (Un collège peut désigner un groupe de personnes partageant une même...) de Li-Sou-Stian (une double anagramme de Lucas d'Amiens , sa ville (Une ville est une unité urbaine (un « établissement humain » pour...) de naissance, et Saint Louis , le lycée où Lucas enseignait).

Sous le titre «  Les brahmes tombent  », Lucas relate que «  N. Claus de Siam a vu, dans ses voyages pour la publication des écrits de l'illustre Fer-Fer-Tam-Tam, dans le grand temple de Bénarès, au-dessous du dôme qui marque le centre du monde (Le mot monde peut désigner :) , trois aiguilles de diamant (Le diamant est un minéral composé de carbone (tout comme le graphite et la...) , plantées dans une dalle d'airain, hautes d'une coudée (La coudée (lat. cubitus) est une unité de longueur vieille de plusieurs milliers d'années. Elle...) et grosses comme le corps d'une abeille (Abeille est un nom vernaculaire ambigu désignant en français certains insectes...) . Sur une de ces aiguilles, Dieu enfila au commencement des siècles, 64 disques d'or pur, le plus large reposant sur l'airain, et les autres, de plus en plus étroits, superposés jusqu'au sommet. C'est la tour sacrée du Brahmâ. Nuit et jour (Le jour ou la journée est l'intervalle qui sépare le lever du coucher du Soleil ; c'est la...) , les prêtres se succèdent sur les marches de l'autel, occupés à transporter la tour de la première aiguille sur la troisième, sans s'écarter des règles fixes que nous venons d'indiquer, et qui ont été imposées par Brahma. Quand tout sera fini, la tour et les brahmes tomberont, et ce sera la fin des mondes !  ».

Comme indiqué ci-dessous, un jeu à 64 disques requiert un minimum de 2 64 -1 déplacements. En admettant qu'il faille 1 seconde ( Seconde est le féminin de l'adjectif second, qui vient immédiatement après le premier ou qui...) pour déplacer un disque, ce qui fait 86 400 déplacements par jour (Le jour ou la journée est l'intervalle qui sépare le lever du coucher du Soleil ; c'est la...) , la fin du jeu aurait lieu au bout d'environ 213 000 milliards de jours, ce qui équivaut à peu près à 584,5 milliards d'années, soit 43 fois l'âge estimé de l' univers (L'Univers est l'ensemble de tout ce qui existe et les lois qui le régissent.) (13,7 milliards d'années selon certaines sources).

Résolution récursive

Le problème des tours de Hanoï est vu en algorithmique (L'algorithmique est l’ensemble des règles et des techniques qui sont impliquées...) (programmation), où il offre un exemple de la puissance (Le mot puissance est employé dans plusieurs domaines avec une signification particulière :) et de la lisibilité des programmes définis de façon récursive (un autre exemple étant le tri arborescent). En effet, la méthode de résolution vue (La vue est le sens qui permet d'observer et d'analyser l'environnement par la réception et...) précédemment conduit à un algorithme récursif (Les algorithmes récursifs et les fonctions récursives sont fondamentaux en informatique....) , décrit ci-dessous. Les paramètres de la procédure Déplacer sont :

On obtient par exemple :

En langage PHP

En langage Python  :

En langage Prolog  :

• Énigmes
• Conférences

Les tours de Hanoï

Selon une légende très ancienne, il existe un temple où les moines sont chargés de veiller sur 64 disques sacrés. Les disques, qui sont tous de taille différente, forment une tour. Comme ils sont précieux et très fragiles, un disque ne peut être placé sur un disque plus petit.

Hélas, le jour vient où quelques travaux dans le temple sont nécessaires et les disques doivent être déplacés. Ils sont très lourds et ne peuvent donc être transportés qu'un par un. De plus, il n'y a qu'un seul endroit assez sacré pour les stocker.

Qu'en pensez-vous?

A vous de jouer !

Il existe un jeu basé sur cette légende. Le but du jeu est de bouger tous les disques de la pile du centre vers un nouvel endroit en se servant de la position intermédiaire et en respectant les règles suivantes :

• On ne peut déplacer qu'un disque à la fois.
• On ne peut déplacer un disque qui se trouve sous un autre.
• Un disque ne peut être déposé sur un disque plus petit.

Bien sûr, si n = 1 , un coup suffit ! Si n = 2 , c'est aussi assez facile : On bouge le petit disque en position intermédiaire, puis le grand sur l'endroit final. Enfin, on pose le petit disque sur le grand. Finalement, on a déplacé la pile en 3 coups.

Et si n est plus grand ?

Nous vous proposons de commencer avec 3 disques afin de voir en combien de "coups" vous pouvez déplacer la pile. Quand vous penserez avoir trouvé le nombre de coups minimum, passez à 4 disques. Vous pouvez utiliser le programme JavaScript ci-dessous.

La solution se trouve ici , mais cherchez d'abord !

Au fil des maths

La tour d’hanoï, vive les casse-tête la tour d’hanoï, vous connaissez les auteurs nous présentent ce jeu et s’intéressent à l’aspect mathématique de son fonctionnement reposant sur la numération binaire., michel boutin & frédéric de ligt.

© APMEP Juin 2020

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅♦⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

La Tour d’Hanoï 1 est un casse-tête inventé par le mathématicien français Édouard Lucas (1842-1891) qui en a fait don au Conservatoire national des arts et métiers de Paris 2 en 1888. Ce casse-tête est constitué par une planchette sur laquelle on a fixé trois tiges ; sur l’une d’elles on a enfilé huit disques de diamètres décroissants, le plus petit en haut de la pile et le plus grand en bas.

Figure 1 . Tour d’Hanoï sortie de sa boîte, et installée. © Musée des arts et métiers, Cnam, Paris / Photo Michèle Favareille .

L’objectif du joueur est de transposer tous les disques d’une tige à une autre en respectant des règles de déplacement très précises : à chaque coup, le joueur prend un disque sur une tige et l’enfile sur une autre. Celle-ci pourra être soit vide, soit occupée par une pile d’un ou plusieurs disques. Dans ce cas, le joueur ne doit pas recouvrir un disque de diamètre inférieur à celui qu’il est en train de déplacer. Ainsi, un disque, quelle que soit sa grandeur, est toujours posé sur un plus grand que lui.

Un peu d’histoire

La Tour d’Hanoï est le seul jeu inventé par Édouard Lucas qui est entré dans la postérité. La première édition fut commercialisée en 1883 avec ce titre très curieux et apparemment très mystérieux : «La Tour d’Hanoï véritable casse-tête annamite. Jeu rapporté du Tonkin par le professeur N. Claus (de Siam). Mandarin du Collège Li-Sou-Stian !»

Figure 2 . Boîte de la Tour d’Hanoï. (hauteur : 10 cm, largeur : 14,5 cm, longueur : 15 cm, masse : 365 g.) © Musée des arts et métiers, Cnam, Paris / Photo Michèle Favareille .

Le mystérieux professeur N. Claus (de Siam) fut rapidement identifié : il s’agit de Lucas d’Amiens 3 , professeur au lycée Saint-Louis.

Nombre de déplacements

Dans le fascicule n° 3 de la série «Jeux scientifiques», intitulé «La Tour d’Hanoï, jeu tombé de Saturne» paru en 1889 [2 , 3] sous le chapitre «L’exposant des puissances», Lucas donne une méthode simple pour calculer le nombre \(N\) de déplacements selon le nombre \(n\) d’étages : \(N=2^n-1\) .

Figure 3. Page de titre du livret « Jeux scientifiques n° 3 » : La Tour d’Hanoï.

Pour une tour de \(8\) étages, on a \(2^8 – 1 = 255\) déplacements. Pour une tour de \(64\) étages, on a un nombre de manœuvres égal à \(2^{64} – 1\) , c’est un nombre de \(20\) chiffres. Cette valeur étant fastidieuse à calculer au XIXe siècle, Lucas donne un moyen pour connaître le nombre de chiffres du résultat : \(\text{E}\left(\log(2^{64})\right)+1\) , où \(\text{E}(x)\) désigne la partie entière de \(x\) . Dans le même fascicule, il justifie mathématiquement la formule proposée pour le nombre de déplacements de la Tour d’Hanoï comportant \(3\) tiges et \(n\) disques.

Quel que soit le nombre de disques, le plus grand d’entre eux n’est déplacé qu’une seule fois, mais le reste de la tour doit changer deux fois de tige, la première fois pour libérer le disque le plus bas et la seconde pour le recouvrir sur une autre tige. Ainsi, la totalité des déplacements, pour une tour de \(n\) disques est toujours égale à la somme de \(1\) déplacement (celui du grand disque) et de deux fois le nombre de déplacements correspondants à une tour de \(n – 1\) disques. Par exemple pour \(4\) disques, on a les trois plus petits à déplacer ( \(7\) coups), puis le plus grand disque ( \(1\) coup), puis une seconde fois les trois plus petits ( \(7\) coups). On a donc \(N_4 = 7 + 1 + 7 = 15\) déplacements. Ainsi \(N_n = N_{n-1} + 1 + N_{n-1} = 1 + 2N_{n-1}\) . Cette relation permet d’initier une suite récurrente dont la conclusion permettra d’établir une relation mathématique pour calculer directement le nombre de coups à effectuer pour déplacer \(n\) disques d’une tige à une autre : \(N_n = 2^n- 1\) .

Codage binaire et ternaire des déplacements

Le déplacement des disques suit inéluctablement un protocole précis qui fut décrit dès 1884 par le petit-neveu d’Édouard Lucas, Raoul Olive : «Pour monter la tour sur trois tiges, quel que soit le nombre d’étages, il faut faire continuellement tourner le disque le plus petit, toujours dans le même sens de rotation circulaire tous les deux coups» . En respectant ce protocole, la suite des déplacements peut être exprimée par une suite de nombres binaires dont le nombre de chiffres est égal au nombre de disques. La suite des nombres binaires qui correspond à celle des décimaux est appelée code binaire naturel.

Figure 4. Code décimal, code binaire naturel. Le binaire naturel est un code pondéré, par exemple : \(6 = 0(2^0) + 1(2^1) + 1(2^2)\) .

Mais on peut organiser une suite de nombres binaires de plusieurs manières dont l’une d’elles, appelée code binaire réfléchi, est caractérisée par ses propriétés d’adjacence : quand on passe d’un nombre au suivant, un seul chiffre binaire change ( \(0\) en \(1\) ou \(1\) en \(0\) ). Cette propriété fut mise à profit en 1872 par un clerc de notaire lyonnais du nom de Louis Gros pour modéliser le fonctionnement du baguenaudier, un autre casse-tête beaucoup plus ancien. Près d’un siècle plus tard, en 1947, un ingénieur américain, Frank Gray, a utilisé ce même code dans un brevet d’invention où il décrit un système capable de transmettre des informations par impulsions électriques pour le compte de la société Bell Telephone Laboratories. Le code binaire réfléchi est connu depuis cette époque sous le nom de code de Gray [4]  .

Figure 5. Code binaire réfléchi (dit code de Gray).

Figure 6. Graphe montrant une propriété du code de Gray : un seul bit (binary digit) change d’état quand on passe d’un sommet à un des trois adjacents, par exemple : de 000 à un des trois sommets 001, 010 ou 100.

Le code de Gray a un intérêt dans de nombreux domaines y compris dans les jeux, en particulier pour modéliser les déplacements des disques de la Tour d’Hanoï. Les déplacements des disques correspondent à une succession de nombres binaires. Considérons une tour à trois disques ( \(\mathsf{d0}\) pour le plus petit, \(\mathsf{d1}\) pour le moyen et \(\mathsf{d2}\) pour le plus grand), et trois tiges ( \(\mathsf{A}\) , \(\mathsf{B}\) , \(\mathsf{C}\) ).

Au départ, les disques sont sur la tige \(\mathsf{A}\) . Sur la figure  7 on montre la succession des sept déplacements à partir de la situation codée \(000\) . Le premier déplacement consiste à transposer le disque \(\mathsf{d0}\) de la tige \(\mathsf{A}\) vers la tige \(\mathsf{B}\) . Cette nouvelle situation est alors codée \(001\) . En effet, seul le disque \(\mathsf{d0}\) a changé de position. La succession des coups pour déplacer la tour d’une tige à une autre revient à écrire le code de Gray quel que soit le nombre de disques.

Le plus petit disque se déplace une fois sur deux, toujours dans le même sens, et les autres sont mis sur la seule tige disponible permettant de ne jamais recouvrir un disque plus petit. En partant de la tige \(\mathsf{A}\) , pour un nombre impair de disques ( \(3\) dans ce cas), si le cycle du petit disque est \(\mathsf{A}\) – \(\mathsf{B}\) – \(\mathsf{C}\) – \(\mathsf{A}\) – \(\mathsf{B}\) alors la position finale de la tour sera la tige \(\mathsf{B}\) ; en partant en sens inverse, \(\mathsf{A}\) – \(\mathsf{C}\) – \(\mathsf{B}\) – \(\mathsf{A}\) – \(\mathsf{C}\) , la tour sera transposée en \(\mathsf{C}\) . Pour un nombre pair de disques le scénario est inversé.

Figure 7 . Codage binaire réfléchi du déplacement des disques pour une tour 3 disques–3 tiges. Le graphe en bas à droite montre le cycle hamiltonien du déplacement des disques ↩ .

La plupart des nombreuses publications au sujet de la Tour d’Hanoï sont des approches mathématiques ; par exemple, les deux articles publiés dans la revue Pour la science , par Jean Lefort  [5] en 2008, et Jean-Paul Delahaye  [6] en 2015, modélisent les déplacements des disques par un graphe, ce qui permet d’indiquer clairement tous les déplacements possibles quelle que soit la phase de jeu. Ils soulignent aussi la correspondance entre la Tour d’Hanoï et les structures fractales. Par exemple, sur la figure 8 , les trois graphes montrent les positions pour trois types de tour avec un disque (I), deux disques (II) ou trois disques (III). Pour trois disques, les sommets du triangle correspondent aux positions des disques de départ ou à l’arrivée : \(\mathsf{AAA}\) si les trois disques sont sur la tige \(\mathsf{A}\) ; \(\mathsf{BBB}\) s’ils sont sur la tige \(\mathsf{B}\) ; \(\mathsf{CCC}\) , sur la tige \(\mathsf{C}\) . Le caractère de droite du code à chacun des sommets indique toujours où se trouve le petit disque \(\mathsf{d0}\) , le caractère central indique la position \(\mathsf{d1}\) , et le caractère de gauche donne la position \(\mathsf{d2}\) , c’est-à-dire du grand disque.

Quelques exemples de déplacements :

\(\mathsf{AAA}\) , les trois disques sont sur la tige \(\mathsf{A}\) ;

\(\mathsf{AAA}\) vers \(\mathsf{AAB}\) , \(\mathsf{d0}\) passe de la tige \(\mathsf{A}\) à la tige \(\mathsf{B}\) ;

\(\mathsf{AAB}\) vers \(\mathsf{ACB}\) , \(\mathsf{d1}\) passe de la tige \(\mathsf{A}\) à la tige \(\mathsf{C}\) ;

\(\mathsf{ACB}\) vers \(\mathsf{ACC}\) , \(\mathsf{d0}\) passe de la tige \(\mathsf{B}\) à la tige \(\mathsf{C}\) .

Deux disques sont alors sur la tige \(\mathsf{C}\) , etc. jusqu’à \(\mathsf{BBB}\) .

Ces graphes indiquent toutes les possibilités pour déplacer la tour d’une tige à une autre. Les plus courts chemins suivent les côtés du triangle. En partant de la tige \(\mathsf{A}\) sur laquelle on a les trois disques \(\mathsf{AAA}\) , si on part à gauche on arrive sur le sommet \(\mathsf{AAB}\) (c’est-à-dire que le petit disque est sur la tige \(\mathsf{B}\) et les autres restent sur la tige  \(\mathsf{A}\) ), si on part à droite on arrive sur le sommet \(\mathsf{AAC}\) (alors le petit disque est sur la tige \(\mathsf{C}\) , et les autres sont restés sur la tige \(\mathsf{A}\) ). En partant du sommet \(\mathsf{AAA}\) on peut aller en \(\mathsf{AAC}\) , puis en \(\mathsf{AAB}\) , etc.

Figure 8. Différents graphes de déplacements. Graphes relatifs aux déplacements pour une tour : un disque (I) ; deux disques (II) ; trois disques (III). Sur ces graphes, le codage des sommets est ternaire. ↩

Par exemple de \(\mathsf{AAA}\) en \(\mathsf{BBB}\) , on peut suivre les sommets \(\mathsf{AAA}\) – \(\mathsf{AAC}\) – \(\mathsf{ABC}\) – \(\mathsf{ABB}\) – \(\mathsf{CBB}\) – \(\mathsf{CBC}\) – \(\mathsf{CAC}\) – \(\mathsf{CAA}\) – \(\mathsf{BAA}\) – \(\mathsf{BAC}\) – \(\mathsf{BBC}\) – \(\mathsf{BBB}\) ; les règles de déplacement sont respectées, mais le chemin suivi n’est pas le plus court. À partir de ces graphes, on voit la naissance d’une structure fractale qui se préciserait en augmentant le nombre de disques.

• Michel Boutin. « Les jeux dans les collections du Conservatoire national des arts et métiers de Paris, 4–La Tour d’Hanoï et le baguenaudier ». In : Le Vieux papier n° 431 (janvier 2019). Planches en couleur IX et X, pp. 25-26. ↩
• Michel Boutin. « Les jeux dans les collections du Conservatoire national des arts et métiers de Paris, 1–Le Jeu icosien (1859) ». In : Le Vieux papier n° 428 (avril 2018). Planche couleur I, pp. 433-441. ↩
• Édouard Lucas. La Tour d’Hanoï, jeu tombé de Saturne. Ce fascicule est le troisième numéro de la collection des « jeux scientifiques » qui en contient six ; tous édités à l’occasion de l’exposition universelle de 1889. Chambon & Baye et Édouard Lucas, Paris, 1889. ↩
• François Sauvageot. « Quadrature ». In : Au fil des maths n° 528 (avril-juin 2018), pp. 55-62. ↩
• Jean Lefort. « La tour de Hanoï, des jeux d’esprit pour la science ». In : Dossier pour la science no 59 (2008), pp. 91-93. ↩
• Jean-Paul Delahaye. « Les tours de Hanoï, plus qu’un jeu d’enfants ». In : Pour la science n° 457 (novembre 2015), pp. 108-114. ↩

Michel Boutin est enseignant en génie électrique à la retraite.

Frédéric de Ligt enseigne les mathématiques au lycée Élie Vinet de Barbezieux.

Cette contribution est extraite d’un article paru dans la revue Le Vieux papier [1] . ↩︎

Le lecteur averti d’aura reconnu l’anagramme de l’auteur. ↩︎

• Browse latest submissions
• By Project-Team
• Technical and Research Reports
• White Papers
• Browse Inria Activity Reports
• X2HAL : batch import
• Software : create the Codemeta.json
• Create your IDHAL
• Create your CVHal
• Haltools : create your publication list
• Haltools : data extraction (Inria only)
• Setting the correct affiliation
• Which version should I submit?
• Choosing the right document type
• Highlight your publications
• Link records on HAL
• Umbrhal Inria for accessibility
• Customise your CVHAL
• Create and Customise your collection
• HAL online help
• Haltools online help
• X2HAL online help
• HAL Video Tutorials
• HAL API Documentation
• Add thumbnails
• Author identifiers (idHAL and CV)
• Adding HAL publications to your ORCID account
• Inria and Open Science

Les Tours de Hanoï : un problème classique de récursion

• UPMC - Université Pierre et Marie Curie - Paris 6 (4 place Jussieu - 75005 Paris - France) 93591
• CNRS - Centre National de la Recherche Scientifique : UMR7606 (France) 441569
• Function : Author
• PersonId : 3794
• IdHAL : christian-queinnec
• IdRef : 02824933X

inria Interstices  :  Connect in order to contact the contributor

https://inria.hal.science/hal-01350294

Submitted on : Friday, July 29, 2016-5:45:31 PM

Last modification on : Tuesday, April 11, 2023-3:16:28 PM

Dates and versions

Identifiers.

• HAL Id : hal-01350294 , version 1

Collections

Algorithme de la Tour de Hanoï : Python, code C++

Qu'est-ce que la Tour de Hanoï ?

La Tour de Hanoï est un puzzle mathématique composé de trois tiges et de nombreux disques superposés. Elle est également connue sous le nom de Tour de Brahma ou Tour Lucas, comme l'a présenté le mathématicien français Edouard Lucas en 1883. Ce puzzle est basé sur des légendes sur le déplacement de disques d'or entre trois tiges.

Ce puzzle comporte trois tiges et un nombre variable de disques empilés. Ces cannes sont conçues comme des tours cycliques. Ainsi, les disques de plus grand diamètre sont empilés en bas et les disques plus petits sont empilés en haut.

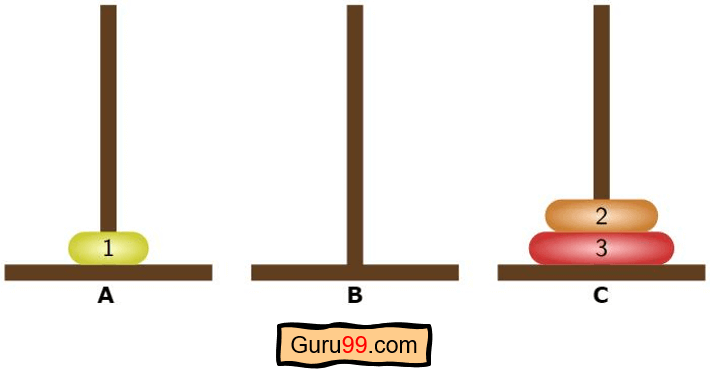
Dans un premier temps, on nous donne trois piquets ou tiges. Et l'un d'eux (A, illustré dans l'exemple) a tous les disques empilés. Notre objectif est de déplacer une pile entière de disques d'une tige (A) à une autre (C) en obéissant à certaines règles spécifiques.

Voici la configuration initiale du puzzle-

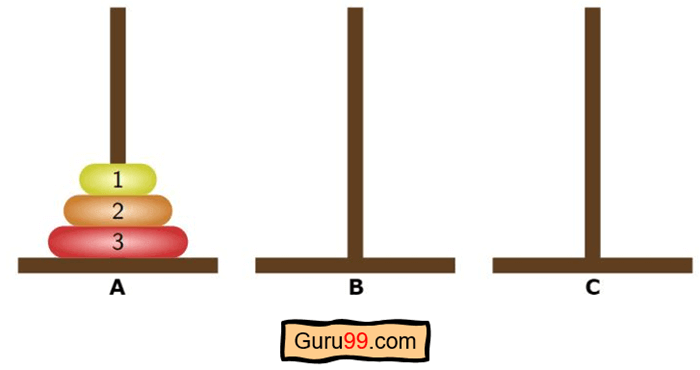
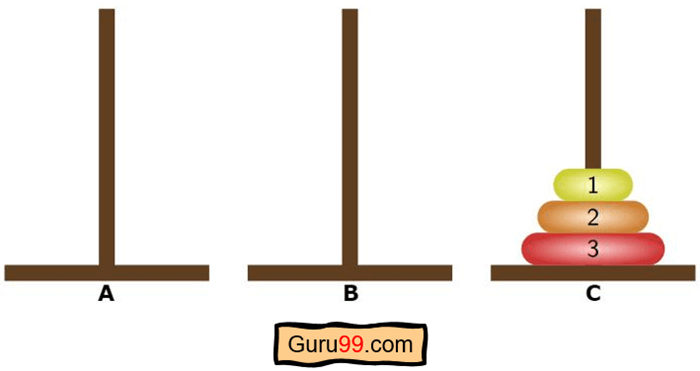
Et c'est le but final-

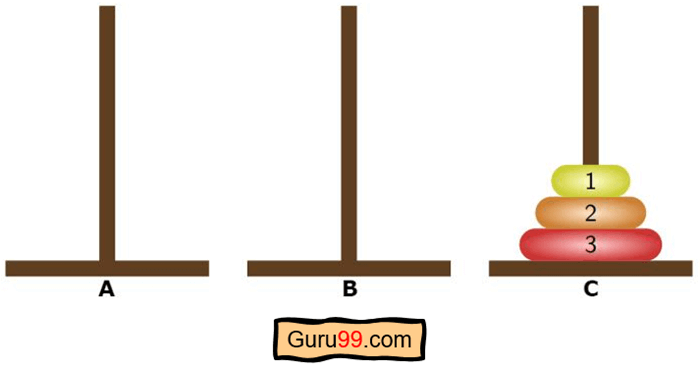
Règles de la Tour de Hanoï

Voici quelques règles essentielles pour la Tour de Hanoï :

• L'état initial de ce puzzle, tous les disques seront empilés dans la première tige.
• L'état final est que tous les disques de la tige un seront empilés sur la tige deux ou sur la tige trois.
• Nous pouvons déplacer un disque d’une tige à une autre à tout moment.
• Nous ne pouvons déplacer que le disque supérieur de la tige.
• Un disque ne peut pas être placé sur un autre disque, plus petit.

La légende originale parlait du déplacement de 64 disques. Les prêtres pouvaient déplacer un disque à la fois selon les règles. Selon la légende, il y avait une prophétie selon laquelle le monde prendrait fin s'ils parvenaient à accomplir l'acte. Au moment venuplexDans la section Ville, nous montrerons qu'un réglage de la Tour de Hanoï avec n disques coûterait 2 ^ n – 1 coup.

Ainsi, si les prêtres pouvaient avoir besoin d'une seconde pour déplacer les disques, le temps total dont ils auraient besoin pour résoudre le puzzle serait de 1 ^ 2 – 64 seconde ou 1 584,942,417,356 26 7 ans, jours, hours, et 15 secondes.

Algorithme pour la Tour de Hanoi

Une manière générale de résoudre la Tour de Hanoï est un algorithme récursif. Tout d’abord, nous devons choisir deux tiges ou piquets comme source et destination, et le piquet de rechange serait un auxiliaire ou une aide.

Voici les étapes pour résoudre le puzzle de la Tour de Hanoï :

• Déplacez les n-1 premiers disques du rattachement source vers le rattachement auxiliaire.
• Ensuite, déplacez le nième disque du rattachement source vers le rattachement de destination.
• Enfin, déplacez les n-1 disques restants de la cheville auxiliaire vers la cheville de destination.

Notes : Si nous avons un seul disque, nous pouvons le déplacer directement de la source à la destination.

Comment résoudre le puzzle de la Tour de Hanoi

Illustrons l'algorithme pour trois disques et considérons la cheville A comme source, la cheville B comme assistant et la cheville C comme destination.

Étape 1) Initialement, tous les disques seront empilés sur le plot A.

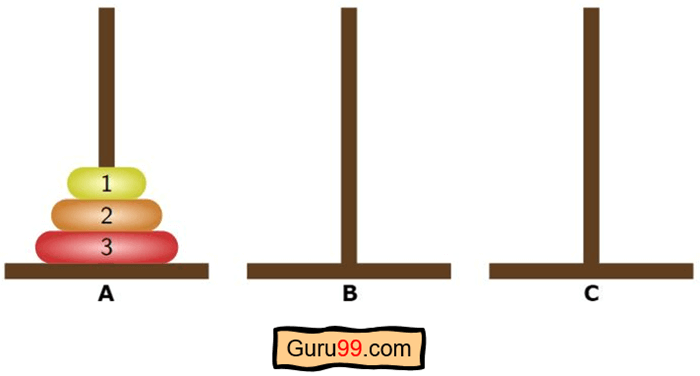
À ce stade:

Source = cheville A Destination = cheville C Aide = cheville B

Maintenant, nous devons déplacer les n-1 premiers disques de la source vers l'assistant.

Remarque: Bien que nous ne puissions déplacer qu'un seul disque à la fois, cela fait passer notre problème d'un problème à 3 disques à un problème à 2 disques, ce qui est un appel récursif.

Étape 2) Comme nous appelons un appel récursif depuis le piquet A et que la destination est le piquet B, nous utiliserons le piquet C comme assistant.

Notez que nous sommes à nouveau à la première étape pour le même problème de tour de Hanoi pour deux disques.

Nous devons maintenant déplacer n-1 ou un disque de la source vers l'assistant, en déplaçant le plus petit disque de la cheville A à la cheville C.

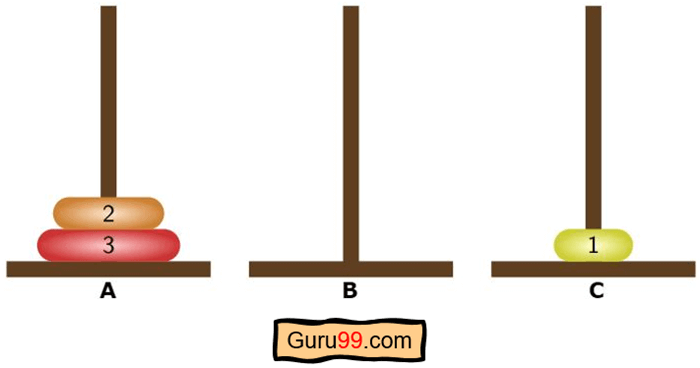
Source = cheville A Destination = piquet B Aide = cheville C

Étape 3) Ensuite, selon notre algorithme, le nième ou le deuxième disque nécessaire doit être transféré vers la destination ou le chevillement B.

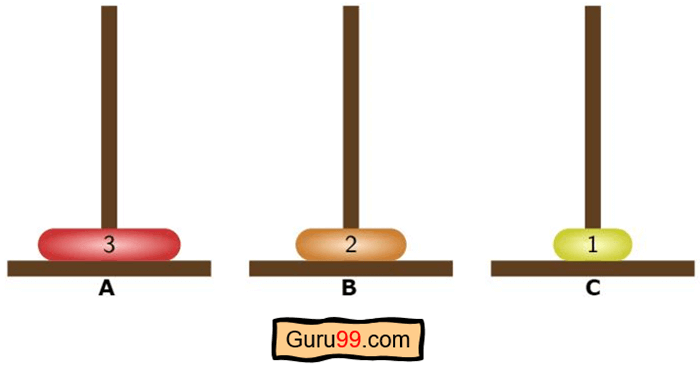
Étape 4) Maintenant, nous allons déplacer les n-1 disques ou le disque un de l'assistant ou du chevillement C vers la destination ou le chevillement B selon la troisième étape de notre algorithme.

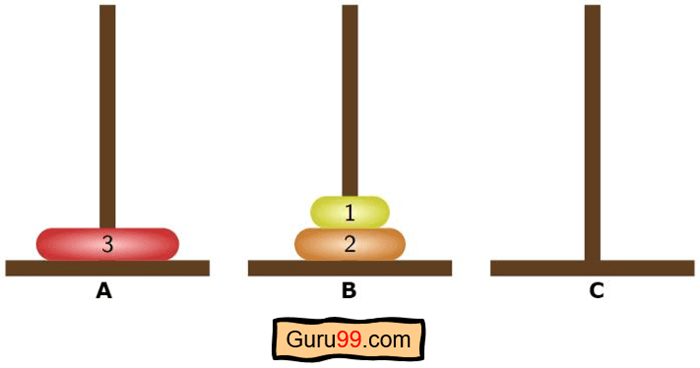
Étape 5) Après avoir terminé l'appel récursif, nous reviendrons à notre paramètre précédent lors de la première étape de l'algorithme.

Étape 6) Maintenant, dans la deuxième étape, nous allons déplacer notre source vers notre destination, qui déplace le disque 3 vers le plot C depuis le plot A.

Source = cheville A Destination = piquet C Aide = cheville B

Étape 7) Maintenant nous pouvons voir ça

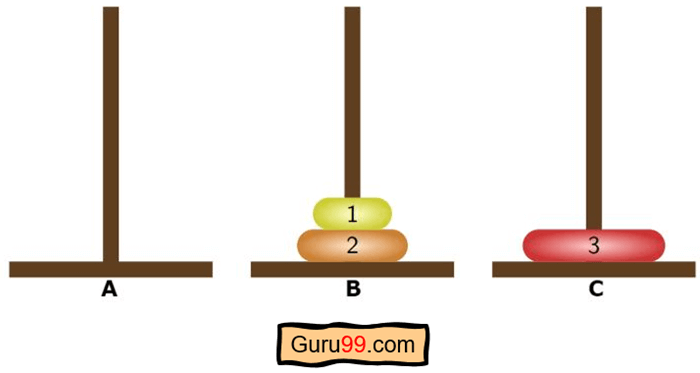
d consiste à déplacer les disques restants de l'assistant (peg B) vers la destination (peg C). Nous utiliserons la source initiale ou le rattachement A comme aide dans ce cas.

Étape 8) Comme on ne peut pas déplacer deux disques simultanémentneohabituellement, nous appellerons un appel récursif pour le disque 1. Selon la dernière étape et notre algorithme , une destination dans cette étape est le piquet A.

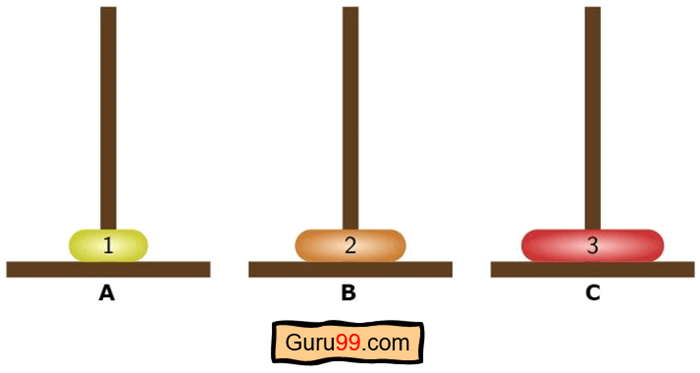
Source = cheville B Destination = piquet A Aide = cheville C

Étape 9) Notre appel récursif est maintenant terminé. Ensuite, nous déplaçons le disque 2 de sa source vers sa destination.

Source = cheville B Destination = piquet C Aide = cheville A

Étape 10) Ensuite, nous déplaçons notre n-1 ou disque 1 restant de l'assistant vers la destination.

Pseudo-code de la tour de Hanoï

Code de programme en c++, code de programme en python, avecplexville de la tour de hanoï.

Voici le Time and Space Complexville de la Tour de Hanoï :

1) Heure à venirplexité:

Si nous revenons sur notre algorithme, nous pouvons voir que nous introduisons deux fois un appel récursif pour (n-1) disques. Ces appels récursifs pour (n-1) disques peuvent être décomposés en d'autres ((n-1)-1) et ainsi de suite jusqu'à ce que nous n'ayons qu'un seul disque à déplacer.

Pour trois disques-

• Le disque 3 appelle deux fois une fonction récursive pour le disque deux.
• Le disque 2 appelle deux fois une fonction récursive pour le disque un.
• Le disque 1 peut se déplacer dans un temps constant et un temps pour résoudre trois disques.

= 2*(Temps de résolution pour deux disques) + Temps constant pour déplacer le disque 3

= 2*(2*temps pour résoudre un disque + temps constant pour déplacer le disque 2) + temps constant pour déplacer le disque 3

= (2*2) (temps constant pour déplacer le disque 1) + 2*temps constant pour déplacer le disque 2 + temps constant pour déplacer le disque 3

Pour n disques, cela peut s’écrire –

(2 n-1 * temps constant pour déplacer le disque 1 + 2 n-2 * temps constant pour déplacer le disque 2 +….

Cette progression géométrique se traduira par O(2 n-1 ) ou O (2 n ), ce qui est exponentiel.

2) Espace complexity

L'espace complexLa ville de la Tour de Hanoï est 0(n). C'est parce que nous devons stocker la séquence des plaques. Lorsque nous utilisons la récursivité, nous utilisons la pile. Et la taille maximale de la pile peut être « n ». C'est pourquoi l'espace complexity devient O(n).

• Recherche linéaire : Python, exemple C++
• Tutoriel DAA PDF : Conception et analyse de Algorithms
• Algorithme de tri par tas (avec code en Python et C++)
• Algorithme de Kadence : sous-réseau contigu à la plus grande somme
• Algorithme de tri Radix dans la structure de données
• Liste doublement chaînée : C++, Python (exemple de code)
• Liste à chaînage unique dans les structures de données
• Liste de contiguïté et représentation matricielle du graphique

• Recherche par auteur ou oeuvre
• Recherche par idée ou thème
• Recherche par mot clé
• Détecteur de plagiat
• Commande & correction de doc
• Publier mes documents

Consultez plus de 218447 documents en illimité sans engagement de durée. Nos formules d'abonnement

Vous ne trouvez pas ce que vous cherchez ? Commandez votre devoir, sur mesure !

• Matières scientifiques & technologiques
• Mathématiques
• Présentation

Comment résoudre la légende des tours de Hanoï à l'aide de la récurrence ? - Grand Oral de Mathématiques

Thèmes abordés.

Légende des tours de Hanoï, suites, Grand oral , suites récurrentes

Résumé du document

Bienvenue à ce grand oral de la spécialité maths, où nous allons nous intéresser à la résolution de la légende des tours de Hanoï à l'aide de la récurrence, dans le cadre du chapitre des suites. Les tours de Hanoï sont un célèbre puzzle mathématique qui consiste à déplacer une tour de disques d'un piquet de départ à un autre, en utilisant un troisième piquet comme intermédiaire. Cette légende, apparue en 1883, a suscité l'intérêt de nombreux mathématiciens au fil du temps, qui ont cherché à résoudre ce casse-tête. Nous allons voir comment la récurrence peut être utilisée pour résoudre ce problème et comment les suites peuvent être utilisées pour analyser le nombre de déplacements nécessaires pour résoudre le problème en fonction du nombre de disques.

• Comment la récurrence peut-elle être utilisée pour résoudre ce problème ?
• Comment les suites peuvent-elles être utilisée pour analyser le nombre de déplacements nécessaires pour résoudre le problème en fonction du nombre de disques ?

[...] Conclusion En conclusion, nous avons vu comment utiliser la méthode de la récurrence pour résoudre la légende des tours de Hanoï et comment les suites peuvent être utilisées pour analyser le nombre de déplacements nécessaires pour résoudre le problème en fonction du nombre de disques. Nous avons également souligné l'importance de la récurrence dans la résolution de problèmes mathématiques, en particulier dans le domaine des suites. En utilisant cette méthode, nous avons pu trouver une formule générale pour calculer le nombre de déplacements nécessaires pour résoudre le problème avec n disques. Enfin, cette méthode illustre l'importance de la créativité et de la réflexion dans la résolution de problèmes mathématiques, ainsi que la beauté et l'utilité des mathématiques dans la vie quotidienne. [...]

[...] Cette relation peut être établie comme suit : Cas de base : si n = le nombre de coups nécessaires est égal à 1. Cas général : supposons que nous ayons déjà résolu le problème pour n-1 disques. Pour déplacer n disques, nous devons d'abord déplacer les n-1 disques supérieurs sur une tour auxiliaire, puis déplacer le disque n sur la tour de destination, et enfin déplacer les n-1 disques supérieurs sur le disque n. Le nombre total de coups nécessaires est donc égal à 2 fois le nombre de coups nécessaires pour déplacer n-1 disques, plus 1. [...]

[...] Comment résoudre la légende des tours de Hanoï à l'aide de la récurrence ? Introduction Bienvenue à ce grand oral de la spécialité maths, où nous allons nous intéresser à la résolution de la légende des tours de Hanoï à l'aide de la récurrence, dans le cadre du chapitre des suites. Les tours de Hanoï sont un célèbre puzzle mathématique qui consiste à déplacer une tour de disques d'un piquet de départ à un autre, en utilisant un troisième piquet comme intermédiaire. [...]

[...] Pour ce faire, nous allons utiliser la récurrence. La première étape consiste à déplacer les n disques supérieurs de la tour de départ à la tour intermédiaire en utilisant la tour d'arrivée comme tour intermédiaire. Le nombre de déplacements nécessaires est le même que le nombre de déplacements nécessaires pour résoudre le problème à partir de n disques. Ensuite, nous déplaçons le disque restant de la tour de départ à la tour d'arrivée. Le nombre de déplacements nécessaires pour cette étape est 1. [...]

[...] La résolution de la légende des tours de Hanoï à l'aide de la récurrence est basée sur l'étude d'une suite. Cette suite représente le nombre minimal de déplacements nécessaires pour résoudre le problème en fonction du nombre de disques. Pour étudier cette suite, nous allons utiliser la récurrence. Prenons le cas le plus simple où il n'y a qu'un seul disque. Dans ce cas, il suffit de déplacer le disque de la tour de départ à la tour d'arrivée. Le nombre de déplacements nécessaires est donc 1. [...]

• Nombre de pages 3 pages
• Langue français
• Format .docx
• Date de publication 19/06/2023
• Consulté 3 fois
• Date de mise à jour 03/07/2023

Source aux normes APA

Lecture en ligne

Contenu vérifié

Les plus consultés

• Etude et modélisation de la trajectoire d'une balle de tennis
• Analyse de situation de soin relationnel
• Quelle est l'utilité des équations différentielles ? (Sujet de grand oral)
• Comment la convexité permet-elle d'optimiser certains marchés économiques ?
• Comment déterminer l'heure de décès d'un cadavre à l'aide de sa température ? - Grand oral de Mathématiques

Les plus récents

• Évaluation des méthodes d'analyses appliquées aux sciences de la vie et de la santé
• Les probabilités - Définitions de base
• Suites et biodiversité : modéliser l'évolution d'une population
• Spécialité Mathématiques - Les probabilités
• Suites et fonctions

Apprendre les bases de Python pour réussir en N.S.I.

Tours de Hanoï

Difficulté : moyenne

Les tours de Hanoï est un casse-tête composé de trois tours et une pile de disques rangés du plus grand au plus petit comme sur la photo ci-dessous .

Le but est de déplacer la pile de disques sur la tour de droite en ne déplaçant à chaque fois qu'un seul disque et un disque ne peut pas être posé sur un disque plus petit. Voici une animation de ce qu'il faut faire dans le cas où il y a 4 disques.

On peut aller voir Wikipédia par exemple pour plus d'informations.

Nous allons voir qu'il est très simple de créer un programme récursif qui nous dit quoi faire pour résoudre le problème. Tout d'abord on appelle les tours A, B et C. On appelle n le nombre de disque présents au départ dans la tour A. Pour déplacer tous les disques de la tour A vers la tour C, on peut raisonner comme suit :

• On déplace n-1 disques de A vers la tour B
• On déplace le dernier disque de A vers C
• On déplace les n-1 disques de B vers C

L'astuce ici est de créer une fonction hanoi qui prend 4 paramètres : hanoi(n,debut,inter,fin) où n est le nombre de disques à déplacer, debut est la tour de départ de nos n disques, inter est la tour intermédiaire que l'on peut utiliser pour déplacer et fin est la tour ou doivent se trouver les n disques au final.

Ainsi, au début on va lancer hanoi(n,"A","B","C") mais quand on va vouloir déplacer les n-1 disques de A vers B, on écrira hanoi(n-1,"A","C","B") .

Ecrire cette fonction recursive hanoi(n,debut,inter,fin) de manière à afficher (avec print ) à chaque étape le déplacement à effectuer sous la forme "A B" pour un déplacement de la tour "A" vers la tour "B" par exemple.

Entrée : (n,"A","B","C") où n est un entier.

Sortie : Les instructions à suivre pour déplacer les n disques de la tour "A" à la tour "C" donnée sous la forme "A B" pour signifier un déplacement de A vers B et affiché avec print .

The #1 tech hiring platform

Analyse de complexité temporelle | Tour de Hanoï (Récursivité)

Tour de Hanoï est un puzzle mathématique où nous avons trois tiges et n disques. L’objectif du puzzle est de déplacer la pile entière vers une autre tige, en respectant les règles simples suivantes :  1) Un seul disque peut être déplacé à la fois.  2) Chaque déplacement consiste à prendre le disque supérieur d’une des piles et à le placer au-dessus d’une autre pile, c’est-à-dire qu’un disque ne peut être déplacé que s’il s’agit du disque le plus haut d’une pile.  3) Aucun disque ne peut être placé sur un disque plus petit. 

Pseudocode   

Analyse de la récursivité 

pour 5 disques soit n=5 Il faudra 2^5-1=31 coups.

Post automatically translated

Article written by Shubham Pandey 5 and translated by Acervo Lima. The original can be accessed here . Licence: CCBY-SA

Laisser un commentaire Annuler la réponse

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

Commentaire *

Enregistrer mon nom, mon e-mail et mon site dans le navigateur pour mon prochain commentaire.

Saisissez votre réponse en chiffres cinq + 1 =

708 - La Tour de Hanoï en tant qu’outil cognitif

• March 14, 2012

En psychologie cognitive, dans le domaine de la résolution de problèmes nous avons deux écoles de pensées principales pour l’explication des processus cognitifs impliqués dans cette activité : d’une part l’approche fonctionnaliste de l’école genevoise qui est considérée comme néo-piagétienne et d’autre part l’approche du traitement de l’information. Cependant lorsque nous recherchons des heuristiques efficaces et ce, même au niveau de la recherche, seule la seconde permet de dépasser les difficultés rencontrées. Aussi, dans cet article, nous n’aborderons notre problématique que via ce biais. Dans l’approche de Newell et Simon, le problème surgit de l’écart qui existe entre un état de fait et un état souhaité. Et l’étude de la résolution de problèmes se ramène à celle de la compréhension. Ce processus intègre diverses connaissances dans une représentation mentale qui intègre l’espace du problème et l’ensemble des méthodes activées par la recherche de la solution. Dans ce cadre nous distinguons généralement trois catégories principales de problèmes : ceux de transformation, ceux d’induction de structure et ceux d’arrangements, même si certains problèmes comme le jeu d’échecs sont mixtes et appartiennent à deux catégories. Par contre la tour de Hanoï est un problème de transformation d’état par excellence. L’avantage de ce problème, c’est que son énoncé est élémentaire même pour des élèves en difficultés et que son espace problème est relativement important. Ainsi il offre un spectre d’étude sur le plan cognitif, suffisamment important pour déceler les heuristiques défaillantes, mais surtout pour étudier les choix méthodologiques des testés. En effet, dans ce problème la solution peut être apportée par l’heuristique de réduction de l’écart au but, l’analyse du résolveur général de problèmes, l’analyse régressive ou encore l’analogie. De cette manière, nous pouvons étudier de façon élémentaire la conception de degrés d’abstraction croissants, le déclenchement de règles d’inférences et la mise en oeuvre de stratégies pratiques. La simplicité de ce problème offre aussi la possibilité d’expliciter le polymorphisme des activités mentales sans nécessiter une grande mémoire qui représente un handicap pour les élèves qui ont une déficience au niveau du quotient intellectuel. Comme toutes les étapes du problème sont visuelles, l’élève peut voir de manière interactive ce qu’il effectue aussi il peut corriger en temps réel un choix de trajectoire inopportun ou erroné. Cela permet aussi à l’enseignant de visualiser toutes les étapes de ce processus sans être obligé d’inférer sur les raisons et les choix de l’élève. Cette description explicite et à la fois minimaliste semble très efficace dans le cadre d’apprentissages initiaux mais aussi dans la mémorisation d’un algorithme de résolution. Enfin si ce problème est effectivement inaccessible par l’élève pour une raison spécifique il peut facilement être modifié et simplifié pour se ramener au problème de la tour de Londres qui permet d’engendrer de nombreuses configurations de sous-problèmes. Par cette nouvelle variante, l’enseignant peut mesurer les progrès de son élève quant à son raisonnement et sa manière d’appréhender diverses contraintes. C’est pour l’ensemble de ces raisons que nous conseillons vivement l’exploitation de ce problème pour des enfants en difficultés.

Caméléon | Ελλάς | Expert | GSR | Lygerismes | Perfection | PI | Télémaques Prosfyges

Abel | Archimède | Camus | Carathéodory | Chomsky | Dostoïevski | Einstein | Fraïssé | Galois | Kornaros | Leibniz | Mozart | Sidis | Vincent | Vinci | Vivaldi | Voltaire | Wittgenstein

Advice | Artsakh | Byzance | Chansons | Chronostratégie | Contes | COVID Stats | Droits de l'Humanité | Échecs | Économie | Éducation | Europe | Free Korea | Génocide | Go | Haïku | Hellénisme | Histoire Intelligente | Holodomor | Hua Tou | Hyperstructures | Innovation | Intelligence | Interprétations | Koan | Mathématiques | Missions Musique | Recours européens | Sahara | Stratégie | Tanka | Théâtre | Topostratégie | Urban Design | Western Armenia | ZEE | Zéolithe | Έξυπνη διατροφή

• CONTACTEZ-NOUS

Cours d'algorithmique : LES PILES - LA TOUR DE HANOI

Algorithme 0

• initialiserPile (PILE * p) 
• BOOLEEN <-- pileVide (PILE p) 
• ELEMENT  <--   sommet (PILE p) 
• BOOLEEN  <--   empilerElement (PILE * p, ELEMENT e) 
• BOOLEEN  <--   depilerElement (PILE * p, ELEMENT * e) 

Article plus récent Article plus ancien

Leave a Reply

• Bases de Données
• bureautique
• Courrier Electronique
• Electroniques
• MS- power point
• Ms-Publisher
• Programmation
• Réseaux Informatique
• SGBD ACCESS
• Systèmes d’exploitation
• Tableur - Ms-Excel -
• Traitement de Textes - MS-Word -
• VBA - Excel

Nous sur Facebook

Messages les plus consultés

• Compteurs : exercices corrigés TP bascule JK
• Examen QCM bureautique avec Correction - QCM Word - QCM Excel - QCM PowerPoint - QCM Burautique Corrigé
• Les formulaires en php – exercices corrigés formulaire php5
• Exercices Corrigés Merise : Diagramme de Flux - MCT MOT TPs Analyse Merise : GESTION DES APPROVISIONNEMENTS
• Exercice Corrigé Merise : Diagramme de Flux - MOT -MCT - TP Analyse Merise : Exercices Corrigés Merise : Diagramme de Flux - MCT MOT TPs Analyse Merise : GESTION DES CARTES BLEUES
• QCM corrigé Réseaux Informatiques Examen Réseau avec correction Questionnaire à choix multiple Réseau Quizz Réseaux
• Exercices Corrigés PL/SQL TD SQL Oracle TP Langage PL/SQL ave correction
• Systèmes de numération exo-corrigés
• Examen Bureautique avec Correction : QCM Informatique - QCM Word - QCM Excel - QCM PowerPoint Examen Corrigé Bureautique
• janvier (1)
• février (6)
• décembre (6)
• novembre (9)
• octobre (87)
• septembre (18)
• février (8)
• janvier (4)
• octobre (72)
• septembre (33)
• juillet (5)
• février (47)
• janvier (54)
• décembre (51)
• novembre (87)
• octobre (157)
• septembre (225)

Abonnez-vous pour les mises à jour par mail :